Problema 5 del concurso Olitele 2020
Se dirige a una edad de: 16-17 años

Calcula cuántas soluciones (x, y), que sean pares de enteros positivos, tiene la ecuación 2/x + 6/y = 1.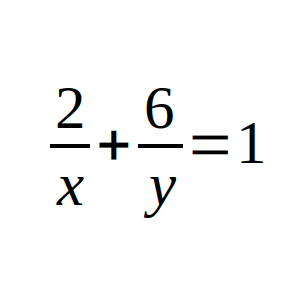
Solución:

Eliminando denominadores mediante la estrategia de multiplicar la ecuación por x y por y, obtenemos 2y + 6x = xy.

Evidentemente, puesto que 2y + 6x es par, uno de los dos factores, x o y, debe ser par.

Si x es par, tomemos x = 2a

Dividiendo por 2 nuestra ecuación, tenemos que y + 6a = ay. Después de intentar varias cosas, he optado por despejar la y:

6a = ay – y

6a = (a – 1)y

6a/(a – 1) = y

Como resulta que debe ser un entero, 6 debe ser divisible entre a – 1, ya que a y a – 1 no tienen divisores comunes:

a = 2, y = 12, x = 4,

a = 3, y = 9, x = 6

a = 4, y = 8, x = 8

a = 7, y = 7, x = 14

Si a = 0, y = 0 (lo que es imposible por el papel que juega y en la ecuación original)

a = -1, y = 3, x = -2

a = -2, y = 4, x = -4

a = -5, y = 5, x = -10

Ahora, supongamos que x es impar, luego y debe ser par, por lo que y = 2b, x = 2a + 1

La igualdad 2y + 6x = xy se transforma en 4b + 12a + 6 = 4ab + 2b, es decir, b + 6a + 3 = 2ab, por lo que 2ab – b = 6a + 3, por lo que b(2a – 1) = 3(2a + 1), y b = 3(2a + 1)/(2a – 1), así que 2a – 1 debe dividir a 3, ya que 2a + 1 y 2a – 1 no tienen de nuevo divisores comunes, por lo que tenemos las posibilidades siguientes:

a = 2, b = 5, x = 5, y = 10

a = 1, b = 9, x = 3, y = 18

a = 0, b = -3, x = 1, y = -6

a = -1, b = 1, x = -1, y = 2

La soluciones, por tanto, son 11:

(-1, 2), (1, -6), (3, 18), (5, 10), (-10, 5), (-4, 4), (-2, 3), (14, 7), (8, 8), (6, 9) y (4, 12)