Problema 6 de la Fase Local de la Olimpiada Española de Matemáticas 2021
Se dirige a una edad de: 16-17 años

ABCD es un cuadrilátero convexo, que verifica AB > BC, CD = DA, y el ángulo ABD es igual que el ángulo DBC.

Sea E el punto de la recta AB tal que el ángulo DEB es un ángulo recto.

Prueba que AE = (AB – BC)/2.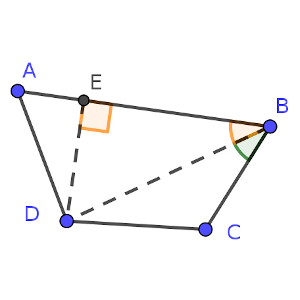
Solución:

Una de las claves para este tipo de problemas es cómo realizas la construcción.

Si tenemos dos lados iguales (que además, comparten un vértice), podemos trazar una circunferencia de la que ambos lados serían radios.

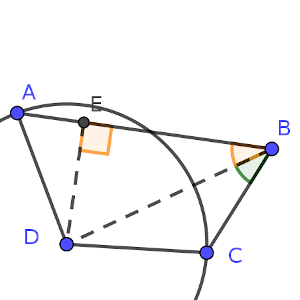
En un principio, podríamos pensar que el punto A puede ser cualquiera de los dos en los que la circunferencia corta a la recta AB, pero veremos que no puede ser así más adelante.

Ahora, observamos que la diagonal DB es la bisectriz de el ángulo ABC, según las condiciones del problema, por lo que uno de los puntos de intersección entre la recta AB y la circunferencia sería el simétrico de C respecto a esta diagonal, que llamaremos C’.

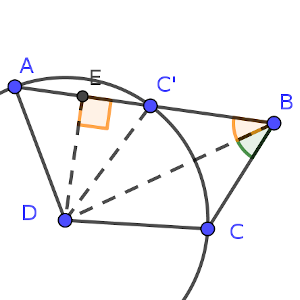
Ese punto pertenece a la circunferencia por razones de simetría (D es el centro de la circunferencia) y, evidentemente, era el otro candidato a ser A, pero no puede ser, puesto que en ese caso, AB sería igual que BC por simetría, en contra de lo que afirma el enunciado.

Ahora bien, dada la construcción de E como perpendicular a la recta AC’ = recta AB, está a la misma distancia de A que de C’, puesto que es la altura de un triángulo isósceles (DC’ y DA son radios de la misma circunferencia).

Por lo tanto está claro que BC = BC’ por simetría, y AE = AC’/2, por lo que AE = (AB – BC’)/2 = (AB – BC)/2, que es lo que debíamos demostrar.