Problema 8 de la Fase Local de la Olimpiada Española de Matemáticas 2021
Se dirige a una edad de: 16-17 años

Determinar todas las funciones f tales que f(xf(y) + y) = f(xy) + f(y) para todos los números reales x, y.

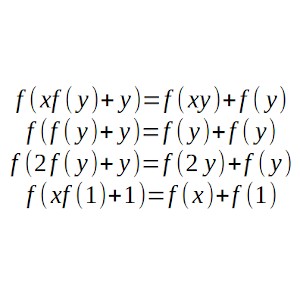
Solución:

Las ecuaciones funcionales son toda una categoría en esta competición.

En este caso, se trata de una igualdad que tiene sumas y multiplicaciones, y que se cumple para todos los valores reales. Suele ser útil ver qué significa para valores particulares de x e y que tengan propiedades relevantes para la multiplicación y la suma, como por ejemplo el 0.

En efecto, si obligamos a que x = y = 0, tenemos que f(0) = f(0) + f(0), lo que nos lleva a que f(0) = 0.

En particular, si suponemos que f(x) = 0 para todo x, se cumple la ecuación, por lo que es sencillo dar con una solución.

Ahora bien, supongamos que no es cierto que sea una función constante, y veamos qué más podemos conseguir.

Después de trastear otros valores y no conseguir nada relevante, nos preguntamos ¿habrá otro valor t no nulo de forma que f(t) = 0? Si lo hay, tomando y = t, tendríamos que f(t) = f(xt) + f(t), con lo que f(xt) sería 0 para cualquier x, y eso es imposible, ya que si t no es nulo, cualquier número puede construirse como xt.

Es decir, que si f no es constante, sólo hay un valor que da 0. Si volvemos a ver la igualdad, observamos que es una igualdad en la que hay una f aplicada en un punto y dos f sumadas en el otro.

Ya nos hemos planteado qué pasaría si el punto donde está tomada la función de un lado coincide con el segundo, es decir, si xf(y) + y = y, pero qué pasaría si xf(y) + y coincide con xy, es decir, qué pasaría si xf(y) + y = xy. Lo que sucede es que y = xy – xf(y), por lo que y = x(y – f(y)), y entonces podrían suceder dos cosas, o f(y) = y, con lo que y = 0, o bien x = y/(y – f(y)).

Veamos qué pasa si probamos a sustituir este valor en la fórmula, ya que una parte de la igualdad coincide con el otro extremo entero.

Esto quiere decir, que si para algún valor no nulo (en 0 ya sabemos que f(0) = 0) es diferente y de f(y), podemos construir una x que valga y/(y – f(y)), y al sustituirla en nuestra igualdad, tendremos que f(f(y)y/(y – f(y)) + y) = f( f(y)y/(y – f(y)) + y(y – f(y))/(y – f(y))) = f(y²/(y – f(y))), pero según nuestra igualdad inicial, eso es f(xy) + y = f(y²/(y – f(y))) + f(y), es decir, que f(y) = 0, y por tanto y es nulo, en contra de la hipótesis.

Eso quiere decir que siempre sucede que y = f(y), es decir, que se trata de la función f(x) = x, que también cumple la igualdad (en efecto, f(xf(y) + y) = f(xy + y) = xy + y, que es igual a f(xy) + f(y)).

Por lo tanto las dos únicas funciones que cumplen la igualdad son f(x) = 0 y f(x) = x.