Problema 1 del nivel A de la Olimpiada Autonómica de la Comunidad Valenciana
Se dirige a una edad de: 12-13 años

Si (a + 1/a)² = 5, ¿cuánto vale (a³ + 1/a³)²?

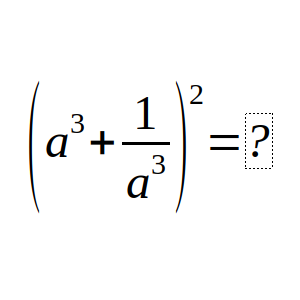
Solución:

Empecemos por desarrollar un poco la expresión (a + 1/a)² = 5. Si nos fijamos bien, resulta que da a² + 2 + 1/a² = 5, es decir, a² + 1/a² = 3.

Para el resto de razonamiento, podemos suponer que a + 1/a = raíz(5). Cambiar signos supondría algunos cambios, pero no demasiados.

Y esto puede dar una idea muy oportuna, ya que (a + 1/a)³ se puede parecer a la expresión que queremos, que está dentro del cuadrado, ya que al multiplicar la a² + 1/a² = 3 por a + 1/a = raíz(5), obtenemos a³ + 1/a³ + a + 1/a = 3raíz(5).

Puesto que a + 1/a = +raíz(5), como (a + 1/a)³ es +-5·raíz(5), resulta que a³ + 1/a³ + raíz(5) = +3·raíz(5), es decir, a³ + 1/a³ = +2·raíz(5).

De esta forma (estudiando los dos posibles signos, tenemos que a³ + 1/a³ = +-2·raíz(5)), (a³ + 1/a³)² = 4·5 = 20.

Otra manera mucho más difícil de hacerlo es calcular (de forma aproximada) el valor de a y usar la calculadora para calcular el valor solicitado.