Problema 3 del nivel A de la Olimpiada Provincial de Alicante de la Olimpiada de la Comunidad Valenciana de 2023
Se dirige a una edad de: 12 -13 años

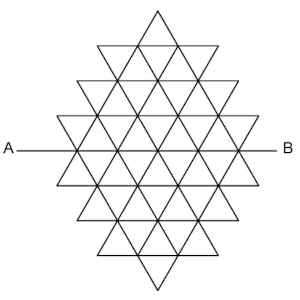
Cada una de las dos mitades de la siguiente figura está compuesta por 22 triángulos pequeños, de los cuáles hay coloreados 4 de rojo, 6 de amarillo y 12 de verde.

Al doblar la figura por la recta AB resulta que quedan superpuestos tres pares de triángulos rojos, cuatro pares de amarillos y dos pares rojo/verde, no habiendo más parejas de estos tipos.

¿Cuántos pares de triángulos verdes coinciden?

Solución:

En esta ocasión se trata de un problema muy sencillo, en el que es suficiente contar cuántos triángulos se unen a los de un color determinado.

En total hay 44 triángulos, 8 rojos, 12 amarillos y 24 verdes.

Cuando doblamos la figura, los pares rojos utilizan 6 de los rojos, y los pares rojo/verde utilizan los dos restantes, de forma que no quedan más disponibles.

Los pares amarillos utilizan 8 de los amarillos, de forma que quedan cuatro que no pueden emparejarse con rojo ni con amarillo, por lo que se emparejarán con cuatro verdes.

Así que, de los 24 verdes hay 2 emparejados con los rojos, cuatro con los amarillos y el resto (18) entre sí, así que se forman nueve parejas verdes.