Problema 3 del nivel B de la Olimpiada Provincial de Alicante de la Olimpiada de la Comunidad Valenciana de 2023
Se dirige a una edad de: 14 -15 años

La figura se ha construido a partir de un triángulo equilátero de lado 2²⁰²² mediante la construcción sucesiva de triángulos equiláteros de lado la mitad del lado anterior.

Calcula el perímetro exterior de la figura, sabiendo que el lado del último triángulo dibujado es de longitud 2⁰ = 1.

Pista: 1 + 2 + 4 +… + 2^n = 2^(n + 1) – 1.

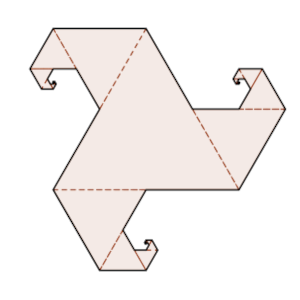
Solución:

Si añadimos un único triángulo en cada lado del original, en realidad, estamos añadiendo 3 lados de tamaño la mitad que el original, ya que añadimos seis lados pero quitamos 3 de ese tamaño.

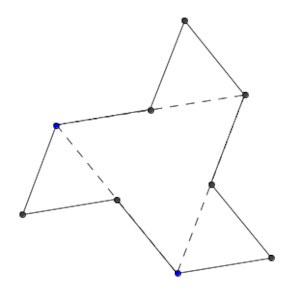
De esa forma, cada paso que demos estaremos añadiendo la mitad del perímetro, así que la suma de todos los pasos sería 3·2²⁰²² + 3·2²⁰²¹ + … + 3.

Si sacamos el factor 3 como factor común, y aplicamos la fórmula que nos da el problema, el total sería 3·(2²⁰²³ – 1).