Problema 2 de la Fase Local de la Olimpiada Española de Matemáticas 2024 (viernes)
Se dirige a una edad de: 16-17 años

Sea P(x) un polinomio de grado 5, y sean a y b dos números reales diferentes de 0.

Supongamos que el resto de P(x) al dividirlo por x³ + ax + b es igual al resto al dividirlo por x³ + ax² + b.

Determinar el valor de a + b.

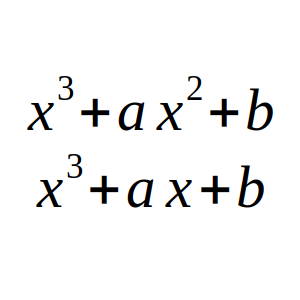
Solución:

El paso clave es entender que, si P(x) tiene el mismo resto al dividirlo entre ambos polinomios, existen dos polinomios cociente, que son de grado 2, que cumplen la relación fundamental en la división, con el mismo polinomio resto. Supongamos que uno de ellos es c(x) y el otro es q(x) (recuerda que ambos son de segundo grado).

Tenemos por tanto que P(x) = (x³ + ax + b)c(x) + r(x) y también P(x) = (x³ + ax² + b)q(x) + r(x).

Por lo tanto, P(x) – r(x) se puede factorizar de dos formas diferentes: (x³ + ax + b)c(x) = (x³ + ax² + b)q(x).

Pero sabemos que un polinomio de grado 5 sólo tiene una factorización, como sucede con los números enteros (salvo, a lo sumo, factores reales, por los que podemos dividir para que ambos tengan primer coeficiente 1).

Y como estos factores, bien son de grado 2 o de grado 1, existe al menos uno de los factores que divide tanto a x³ + ax + b como a x³ + ax² + b, ya que claramente c(x) y q(x) deben ser polinomios diferentes y no pueden tener los mismos factores.

Si divide a ambos, divide a la diferencia, es decir, que divide a ax² – ax = a(x² – x) = ax(x – 1).

Sin embargo, x no puede ser uno de los factores que divide, porque eso significaría que 0 es raíz de ambos polinomios, x³ + ax + b y de x³ + ax² + b, y eso significaría que b vale 0. Por lo tanto, sólo nos queda la posibilidad de que el polinomio que divide a ambos tenga el factor (x – 1).

Por último, eso significa que ambos polinomios tienen la raíz 1, es decir, que 1³ + a·1 + b = 0 y que 1³ + a·1² + b = 0. Evidentemente, ambas expresiones son equivalentes, y nos garantizan que 1 + a + b = 0, por lo que a + b debe valer -1.

En este problema, es fácil caer en la tentación de tratar de averiguar exactamente cuáles son los coeficientes de c(x) y q(x) por la igualdad, pero el sistema tiene demasiados grados de libertad y resulta confuso el sistema que se produce, aún en el caso de que establezcamos que el coeficiente principal (el de x²) vale 1 en ambos casos. Nos queda un sistema con 5 ecuaciones y 6 incógnitas, y, aunque algunas son sencillas de determinar en función de un parámetro, con otras no sucede, y no he conseguido que me determinen el valor de a + b, aunque sospecho que es posible hacerlo.

Otra cosa que me pregunto es si podré construir un par de valores a y b para los que estas igualdades funcionen.

Imaginemos, por ejemplo, a = 2, b = -3.

El polinomio x³ + 2x – 3 es divisible por x – 1, si probamos a dividirlo obtendremos x³ + 2x – 3 = (x – 1)(x² + x + 3).

Por otro lado, x³ + 2x² – 3 también lo es, y de nuevo factorizando, tenemos que x³ + 2x² – 3 = (x – 1)(x² + 3x + 3).

Utilizando estos dos factores tenemos que (x³ + 2x – 3)(x² + 3x + 3) = (x³ + 2x² – 3)(x² + x + 3) = x⁵ + 3x⁴ + 5x³ + 3x² – 3x – 9, por lo que el resto al dividir cualquier polinomio que tuviese los coeficientes de términos 5, 4 y 3 iguales o proporcionales a x⁵ + 3x⁴ + 5x³ produciría al dividir por cualquiera de ellos el mismo resto, como se puede comprobar.