Problema 5 del concurso Marató de problemes 2024
Se dirige a una edad de: 14-15 años

Si a, b y c pueden tener como valor tres números reales, diferentes todos ellos de 0, y |x| representa el valor absoluto de x, se pide obtener cuántos valores diferentes puede tener la expresión 4·a/|a|+ 3·b/|b| + 2·c/|c| + a·b/|a·b| + b·c/|b·c| + c·a/|c·a|.

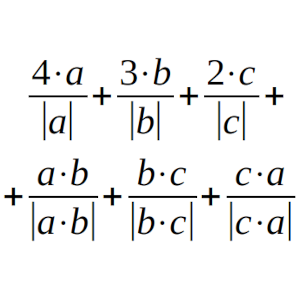
Solución:

Observamos que, puesto que se dividen siempre los números por su valor absoluto, el resultado de los cocientes, salvo los factores 4, 3 y 2, sólo pueden resultar en +1 o -1, según el signo de los números que haya dentro del valor absoluto.

Así que tenemos 8 posibilidades, que estudiaremos por separado, aunque puede que algunas de ellas resulten en valores idénticos.

Todos positivos: resulta 12.

Todos positivos excepto c: 4

Todos positivos menos b: 2

Todos positivos menos a: 0

Todos negativos menos c: -6

Todos negativos menos b: -4

Todos negativos menos a: -2

Todos negativos: -6

Por tanto, podemos obtener 7 valores diferentes.