Problema 6 de la Fase Local (viernes) de la Olimpiada Matemática Española (2018)
Se dirige a una edad de: 16-17 años

Sea AD la mediana de un triángulo ABC de forma que el ángulo ADB es de 45º, y ACB es de 30º.

Determinar el valor del ángulo BAD.

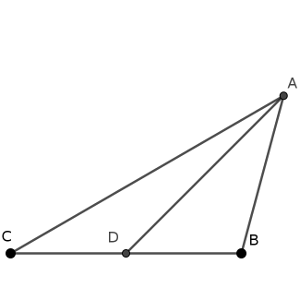
Solución:

Hay muchas aproximaciones diferentes a este problema.

Una muy sencilla de entender es aquella en la que usamos propiedades de los ángulos que nos presentan, es decir, que el ángulo de 45 grados es la diagonal de un cuadrado, y el de 30 grados divide en dos un triángulo equilátero. A partir de ahí, construimos la figura que ilustra este problema y podemos razonar de varias formas.

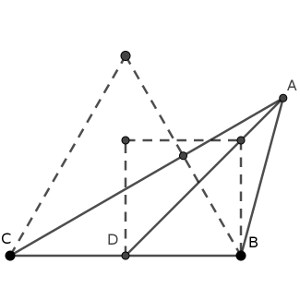
Otra forma de razonar es usando ecuaciones de rectas y sus intersecciones. Para ello, necesitamos construir algunos ángulos y recordar algunos elementos básicos. Suele ser mi aproximación favorita, usando geometría analítica.

Supongamos que la recta que contiene a C, D y B es y = 0, el eje horizontal. Y que la unidad es la mitad de la distancia de C a D, que es a misma que de D a B, por ser D el punto medio de C a B. El punto C podemos ubicarlo en el lugar de coordenadas (0, 0), D es (2, 0) y B es (4, 0). El vector director de la recta AC forma un ángulo con la horizontal de 30º, es decir, puede ser (raíz(3), 1), por lo que la ecuación de la recta que contiene a C y a A sería x – raíz(3)y = 0. El vector director de la recta AD podría ser el (1, 1), y, puesto que contiene el punto (2, 0), sería x – y = 2. La intersección de ambas rectas sería el punto A, que coincide con (raíz(3) + 3, raíz(3) + 1).

Ahora, si hayamos el producto escalar entre AB (1 – raíz(3) , – 1 – raíz(3)) y AD (– 1 – raíz(3) , – 1 – raíz(3)), tendremos 6 + 2·raíz(3), mientras que el módulo de AB sería raíz(8) y el módulo de AD sería raíz(8 + 4·raíz(3)). El resultado de dividir esas expresiones no parece fácil de obtener (recuerda que el coseno del ángulo entre dos vectores es el producto escalar dividido entre el producto de los módulos), pero, si elevamos la fracción al cuadrado, obtenemos exactamente 3/4, luego el coseno del ángulo (que es el resultado de dividir el producto por el producto de los módulos), sería raíz(3)/2, de forma que se trata del ángulo de 30º.

Una tercera forma es dividir el triángulo inicial en cuatro triángulos rectángulos y razonar usando trigonometría básica, aunque necesitaremos alguna fórmula para construir razones poco frecuentes.

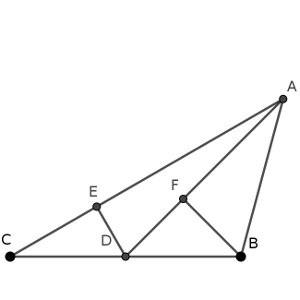
Ahora, si suponemos que los segmentos CD y DB miden ambos 2·raíz(3) (para evitar fracciones en los cálculos), tenemos que ED mide raíz(3), DF mide raíz(6), igual que BF.

Entonces, el ángulo EDF es de 75º = 30º + 45º, y aplicamos para sus razones trigonométricas (necesitamos el coseno) la fórmula de la suma de ángulos, de manera que cos(75º) = cos(30º)·cos(45º) – sen(30º)·sen(45º) = (raíz(6) – raíz(2))/4.

Operando en el triángulo rectángulo AED, resulta que DA = ED/cos(75º) = 4·raíz(3)/(raíz(6) – raíz(2)) = 4·raíz(3)·(raíz(6) + raíz(2))/(6 – 2) = 3·raíz(2) + raíz(6).

Una vez aquí, como DA – DF = FA resulta que FA = 3·raíz(2). Como tenemos que BF medía raíz(6), la tangente del ángulo FAB, que es el que buscamos, es raíz(6)/(3·raíz(2)) = raíz(3)/3 = 1/raíz(3), que corresponde al ángulo de 30º.