Problema 1 de la Olimpiada Matemática Femenina Europea (EGMO 2018) Se dirige a una edad de: 17 años
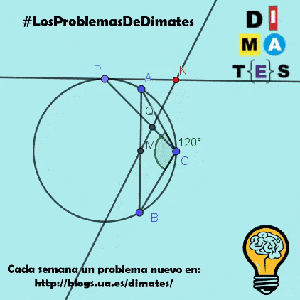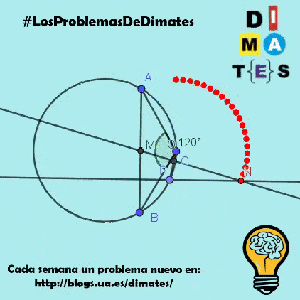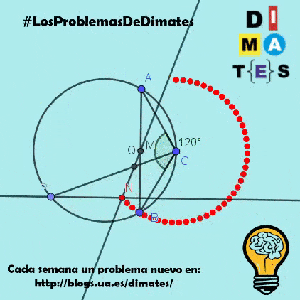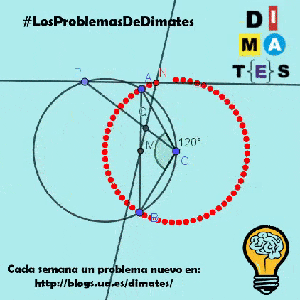
Sea ABC un triángulo de forma que CA = CB y el ángulo ACB mida 120º, y sea M el punto medio de AB.
Sea P un punto variable de la circunferencia que pasa por A, B y C.
Sea Q el punto en el segmento CP tal que QP = 2QC.
Se sabe que la recta que pasa por P y es perpendicular a la recta AB interseca a la recta MQ en un único punto N.
Demuestre que existe una circunferencia fija tal que N se encuentra en esa circunferencia para todas las posibles posiciones de P.