Problema 4 de la Olimpiada Matemática Femenina Europea (EGMO 2018)
Se dirige a una edad de: 17 años

Un dominó es una ficha de 1 x 2 o de 2 x 1 cuadrados unitarios.

Sean n un entero mayor o igual que 3. Se ponen dominós en un tablero de n x n casillas de tal manera que cada dominó cubre exactamente dos casillas del tablero sin superponerse (en otras palabras, sin traslaparse).

El valor de una fila o columna es el número de dominós que cubren al menos una casilla de esta fila o columna.

Una configuración de dominós se llama balanceada si existe algún entero k mayor o igual que 1 tal que cada fila y cada columna tiene valor k.

Demuestre que existe una configuración balanceada para cada n mayor o igual que 3, y encuentre el mínimo número de dominós necesarios para una tal configuración.

Solución:

Me ha parecido un problema precioso, con una dificultad adecuada y que permite ensayar muchas estrategias e ideas interesantes.

Lo normal es manipular tableros pequeños hasta comprender los conceptos implicados y lanzarse después a demostrar.

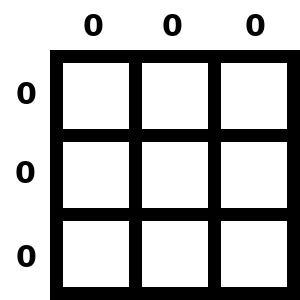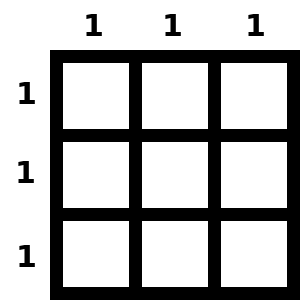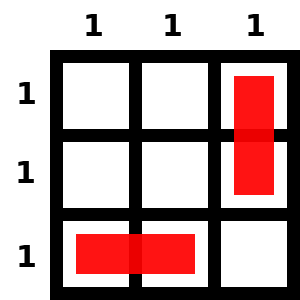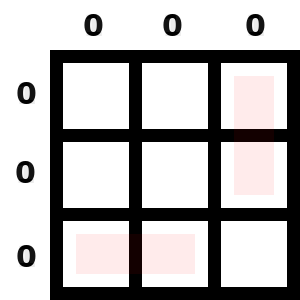
El tablero 3 x 3 lo he trabajado mucho, intentando (y logrando de forma muy sencilla) configuraciones balanceadas de valor 1 y de valor 2. Como se pide la de menor k, evidentemente es 1. Pero es muy interesante ver que también existe la de valor 2, por razones que luego desvelaré.

Antes de empezar, observamos que el número total de filas y columnas que hay es 6 (los valores que hay que tener en cuenta).

En el primer caso he hecho una animación que explica cómo buscar la configuración. Hay un detalle muy importante que debemos observar. Cada vez que añadimos un nuevo dominó, siempre aumenta en 3 unidades la suma de todos los valores de las filas y las columnas, ya que el lado que tiene 2 unidades está en dos filas o dos columnas (por lo que aumenta en 1 cada uno de los valores) y el lado que sólo tiene 1, aumenta el valor de una única fila o columna. Así, la configuración balanceada de valor 1, como tiene que tener como suma de valores 6, sólo tiene 2 dominós.

Para lograr la configuración balanceada de valor 2, debemos tener una suma de valores 6·2 = 12, usaremos 4 dominós, es decir, sólo dejamos un hueco vacío del tablero. He hecho otra animación para que se vea cómo lograrlo a partir de la configuración anterior. Evidentemente, es imposible lograr configuraciones balanceadas con valores mayores.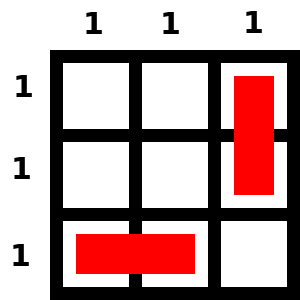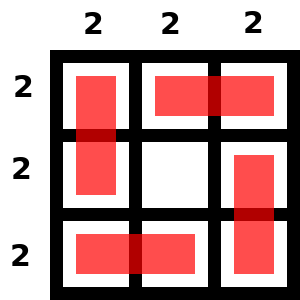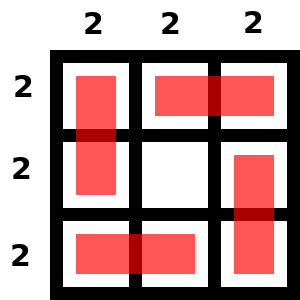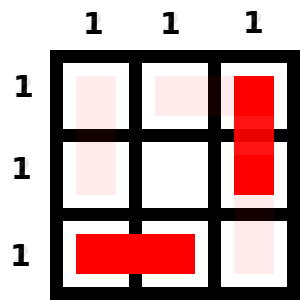

Veamos ahora el tablero de lado 4. Aquí tenemos 8 filas y columnas, de forma que es imposible lograr una configuración balanceada de valor 1 (8 no es múltiplo de 3) y también es imposible lograrla de valor 2 (16 tampoco es múltiplo de 3). Para buscar una de valor 3, tenemos que lograr una suma de los valores de filas y columnas de 24, por lo que necesitaremos 8 dominós, que taparán las 16 casillas del tablero completo.

Tanteando un poco cómo tapar el tablero completo, de forma muy sencilla, encontramos una configuración balanceada, y, claro, de valor 3 (hay dos opciones).

De forma similar, en el tablero de lado 5, con 10 filas y columnas, puesto que 10 y 20 no son múltiplos de 3, tenemos que llegar a valor 3. Necesitamos que la suma de valores llegue a 30, por lo que hay que usar 10 fichas de dominó y tapar 20 de las 25 casillas. Aquí tenemos muchas opciones, yo he optado por partir de la configuración para el tablero de lado 4, añadir una fila y una columna, y hacer algunos cambios, como se puede ver en la animación correspondiente.

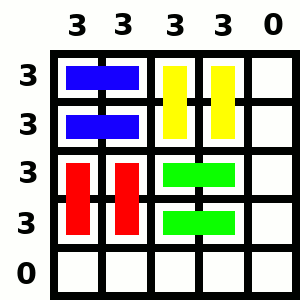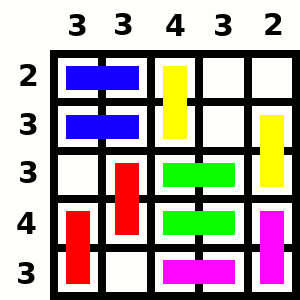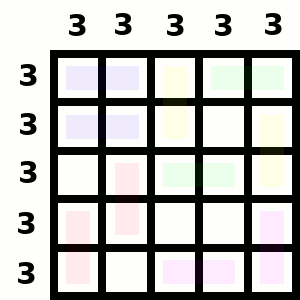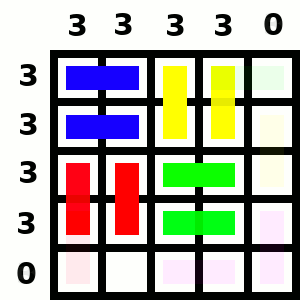
Entonces, para un tablero de lado 5 usamos 10 dominós, y el tablero balanceado tiene valor 3.

Pasemos al tablero de lado 6. Aquí podemos lograr un tablero balanceado de valor 1, ya que 12 es múltiplo de 3. La idea podría ser usar dos tableros de lado 3 balanceados en diagonal, ya que cada fila y cada columna sólo tendrían fichas en la diagonal.

Luego es posible lograr una configuración balanceada de valor 1, usando 4 dominós.

Sin embargo, por razones que luego entenderemos, necesitamos también una configuración balanceada de valor 3, que podemos lograr fácilmente combinando configuraciones de lado 3 de valores 1 y 2 de forma sencilla.

Evidentemente, para esta configuración necesitaremos 3·12/3 = 12 dominós, que taparán 24 de los 36 cuadrados.

El último caso particular que necesitamos trabajar es el tablero de lado 7, con 14 filas y columnas. Por no ser múltiplo de 3, no puede tener configuraciones balanceadas de valores 1 y 2, y la de valor 3 necesita 14·3/3 = 14 dominós. Mi idea, de nuevo, ha sido lograrla a partir del tablero de lado 6 con pocas modificaciones (que también hago como una pequeña animación).

Después de trabajar estos casos individuales, vamos con la demostración propiamente dicha.

Si n es un número múltiplo de 3, de la forma 3p, entonces existe una configuración balanceada de valor 1, un ejemplo de la cual se puede encontrar llenando una diagonal con p configuraciones de tableros de lado 3 (como en el ejemplo correspondiente al 6) de valor 1. Usamos 2p dominós (2n/3).

Si n no es múltiplo de 3, entonces es mayor o igual que que 4 (recordemos que en el problema ya era mayor o igual que 3). No puede tener configuraciones balanceadas de valor 1 ni de valor 2, porque 2n y 4n no serían múltiplos de 3. Para ver que en efecto tiene una configuración balanceada de valor 3, vamos restando 4 unidades hasta llegar a un resultado menor o igual que 7 (será 4, 5, 6 o 7). En una esquina pondremos una configuración balanceada de valor 3, y llenamos la diagonal de configuraciones de tamaño 4 de valor 3. Así logramos una configuración de tamaño n de valor 3, usando 2n·3/3 = 2n dominós.

Por ejemplo, para n = 21, usamos 7 tableros 3×3 balanceados de valor 1, los ponemos en la diagonal y ya está, una balanceada de valor 1.

Otro ejemplo, para n = 22 = 4·4 + 6, ponemos una balanceada de 6×6 de valor 3 en una esquina, y el resto de la diagonal la tapamos con 4 tableros 4×4 balanceados de valor 3, obteniendo una configuración mínima con 8·4 + 12 = 44 dominós (también 44·3/3).