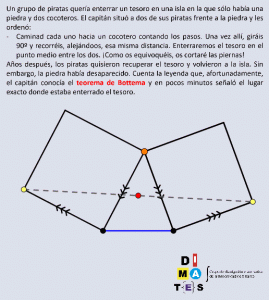
Dos pirámides
Problema propuesto en la prueba PSAT de la Universidad de Princeton, en 1981 Se dirige a una edad de: 16/17
Disponemos de dos pirámides, cuyas caras laterales son todas triángulos equiláteros. Una es de base cuadrada y la otra, de base triangular.
¿Cuántas caras tiene el sólido que formamos si las unimos por una de las caras laterales?
Este problema tiene detrás una curiosa historia, de la que hablaremos cuando pongamos la solución.
Solución: Aquí
Solución a ecuaciones con y sin
Torneo de las ciudades, 2016 (Primavera, nivel A junior) Se dirige a una edad de: 12/15
a) ¿Existen enteros a y b de forma que la ecuación x2 + ax + b = 0 no tiene soluciones reales y la ecuación [x2] + ax + b = 0 sí que tiene al menos una solución real?
b) ¿Existen enteros a y b de forma que la ecuación x2 + 2ax + b = 0 no tiene soluciones reales y la ecuación [x2] + 2ax + b = 0 sí que tiene al menos una solución real?
(La función [k] denota la parte entera de k, es decir, el entero más grande que está por debajo de k.)
Ecuaciones con y sin
Torneo de las ciudades, 2016 (Primavera, nivel A junior) Se dirige a una edad de: 12/15
a) ¿Existen enteros a y b de forma que la ecuación x2 + ax + b = 0 no tiene soluciones reales y la ecuación [x2] + ax + b = 0 sí que tiene al menos una solución real?
b) ¿Existen enteros a y b de forma que la ecuación x2 + 2ax + b = 0 no tiene soluciones reales y la ecuación [x2] + 2ax + b = 0 sí que tiene al menos una solución real?
(La función [k] denota la parte entera de k, es decir, el entero más grande que está por debajo de k.)
Solución: Aquí
Solución a números primos en una ecuación
Olimpiada Iberoamericana de Matemáticas 2016, problema 1. Se dirige a una edad de: 16/17
Encuentra todos los números primos p, q, r, y k tales que pq + qr + rp = 12k + 1.

Números primos en ecuación
Olimpiada Iberoamericana de Matemáticas 2016, problema 1. Se dirige a una edad de: 16/17
Encuentra todos los números primos p, q, r, y k tales que pq + qr + rp = 12k + 1.

Solución: Aquí
Solución a sucesión estancada
Olimpiada Matemática Internacional 2017, problema 1. Se dirige a una edad de: 16/17
Para cada entero a0 > 1, se define la sucesión a0, a1, a2, … tal que para cada n ≥ 0: an + 1 = √(an), siempre que √(an) sea entero, mientras que an + 1 = an + 3 en cualquier otro caso.
Determinar todos los valores de a0 para los que existe un número A tal que an = A para infinitos valores de n.
Sucesión estancada
Olimpiada Matemática Internacional 2017, problema 1. Se dirige a una edad de: 16/17
Para cada entero a0 > 1, se define la sucesión a0, a1, a2, … tal que para cada n ≥ 0: an + 1 = √(an), siempre que √(an) sea entero, mientras que an + 1 = an + 3 en cualquier otro caso.
Determinar todos los valores de a0 para los que existe un número A tal que an = A para infinitos valores de n.

Solución: Aquí
Solución a pesos al azar
Canguro Matemático 2017. Nivel 5 (1º Bachillerato), problema 28. Se dirige a una edad de: 16/17
En una balanza se colocan al azar tres pesos en cada platillo, que queda desequilibrada. La figura muestra lo que sucede. Los pesos eran de 101, 102, 103, 104, 105 y 106 gramos.
¿Cuál es la probabilidad de que el peso de 106 gramos esté en el platillo que pesa más?
Pesos al azar
Canguro Matemático 2017. Nivel 5 (1º Bachillerato), problema 28. Se dirige a una edad de: 16/17
En una balanza se colocan al azar tres pesos en cada platillo, que queda desequilibrada. La figura muestra lo que sucede. Los pesos eran de 101, 102, 103, 104, 105 y 106 gramos.
¿Cuál es la probabilidad de que el peso de 106 gramos esté en el platillo que pesa más?

Solución: Aquí
El Teorema de Bottema
Un grupo de piratas quería enterrar un tesoro en una isla en la que sólo había una piedra y dos cocoteros. El capitán situó a dos de sus piratas frente a la piedra y les ordenó:
-Caminad cada uno hacia un cocotero contando los pasos. Una vez allí, giráis 90º y recorréis, alejándoos, esa misma distancia. Enterraremos el tesoro en el punto medio entre los dos. ¡Como os equivoquéis, os cortaré las piernas!
Años después, los piratas quisieron recuperar el tesoro y volvieron a la isla. Sin embargo, la piedra había desaparecido. Cuenta la leyenda que, afortunadamente, el capitán conocía el teorema de Bottema y en pocos minutos señaló el lugar exacto donde estaba enterrado el tesoro.