Chapter 4: RIGID BODIES III
- ROTATION. CIRCULAR MOTION.
- MOMENT OF A FORCE (TORQUE).
- MOMENT ANGULAR CONSERVATION.
Massachusetts Institute of Technology have developed Open Course Wares (OCW) where you can follow a “Classical Mechanics course” by Internet.
One of the most important magnitudes in architecture is the moment of a force or torque. And this magnitude will be extremely important in Chapter 5: Equilibrium.
Linear momentum, i.e. p = m·v, has a rotational analogue that it is called angular momentum, L. For a symmetrical object rotating about a fixed axis through the centre of mass (CM), the angular momentum is L = I·ω where I is the moment of inertia and ω is the angular velocity about the axis of rotation. The SI units for L are kg·m^2/s, which has no special name.
We saw in Chapter 2: Dynamics laws and applications that Newton’s second law can be written more generally in terms of momentum ΣF = Δp/Δt. In a similar way, the rotational equivalent of Newton’s second law which is Στ = I·α, can also be written more generally in terms of angular momentum Στ = ΔL/Δt where Στ is the net torque acting to rotate the object and ΔL is the change in angular momentum in a interval time Δt.
Angular momentum is an important concept in physics because, under certain conditions, it is a conserved quantity. If Στ = ΔL/Δt on an object is zero then ΔL = 0, so L does not change. This is the law of conservation of angular momentum for a rotating object:
The total angular momentum of a rotating object remains constant if the net torque acting on it is zero.
- A video tutorial about rotation can be watched on the MIT-OCW webpage:
- A video tutorial about the moment of a force/torque can be watched on the MIT-OCW webpage:
- A video tutorial about rotational dynamics can be watched on the MIT-OCW webpage:
- A video tutorial about solved problems can be watched on the MIT-OCW webpages:
Worked example: moment-of-inertia-of-a-disc-from-a-falling-mass
Worked example: massive-pulley-problems
MisConceptual Questions
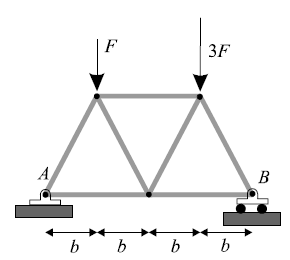
- The symmetric simple truss is loaded as shown in Figure. Which force shown exerts the largest magnitude torque on the truss around point A? And around point B?
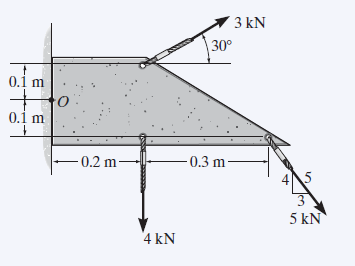
- Calculate the net torque around point O due to the forces acting on the plate shown.
 Video lecture: Rotational dynamic example
Video lecture: Rotational dynamic example
Problem set number 5
- A wheel of radius r = 80 cm has moment of inertia 10 kg·m^2. It is rotating around its central axis propelled by a rocket attached to a point on its outer rim. The rocket is expelling gas
tangentially to the wheel, resulting in a constant force. Determine:- The magnitude of the equivalent force, if we know that the wheel, starting from rest, reaches an angular speed of 1 rev/s in 6 s.
- The value of both tangential and normal acceleration in a point on the outer rim of the wheel.
- The angle that the total acceleration forms with the radius at that point.
- The time that the wheel takes to reach the same angular velocity, under the action of the same force, if we add a very thin ring of mass 5 kg around the outer rim.
If you have some doubts, you can watch next video related to rotational dynamic (Professor Michel van Biezen):
If you were satisfied with this example, you can check more video lectures on the webpage: