Primero y segundo de ESO, Olimpiada Matemática de Secundaria, 2017

Se dirige a una edad de: 12/14 años

Tres parejas se reúnen para comer. Cada persona llega en un momento diferente, y saluda a todos los que están, excepto a su pareja.

Cuando todos están reunidos, uno de ellos pregunta a cada asistente a cuántas personas ha saludado al llegar, obteniendo cinco respuestas distintas.

¿En qué lugar ha llegado la persona que pregunta, que llegó después que su pareja?

Como mínimo se saluda a 0 personas (es decir, a nadie), y como mucho a cuatro, en el supuesto de llegar el último, ya que una de las personas presentes será la pareja de la persona que acaba de llegar.

Como recibe 5 respuestas distintas, debe recibir todas las respuestas posibles, de 0 a 4.

Es evidente que la primera persona saluda a 0 personas, ya que cuando llega no hay nadie. Será miembro de la pareja A.

La segunda persona no puede ser la que ha hecho la pregunta, porque sería de la pareja A, y la siguiente persona no saludaría a uno, sino a dos. Tampoco puede ser de la pareja A, pues tampoco saludaría a nadie, por lo tanto pertenece a otra pareja (pareja B) y saluda a una persona.

La tercera persona tampoco puede ser la que ha hecho la pregunta (de la pareja A o B), pues la siguiente persona sólo puede saludar a dos si fuese la pareja de la otra familia (B o A), y en ese caso, la siguiente saludaría a cuatro personas. Tampoco puede ser la pareja de alguno de los dos, pues de nuevo volvería a saludar sólo a una persona, y no podemos repetir. Luego tiene que ser un miembro de la pareja restante (pareja C), y saluda a dos personas.

La cuarta persona debe ser ya pareja de una de las personas presentes. Pero eso obliga a que salude exactamente a dos personas, así que debe ser la persona que ha hecho la pregunta, y supongamos que es de la pareja A (podría ser de cualquiera de las otras).

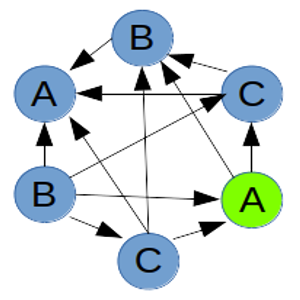
Podemos observar que las dos personas restantes saludan, respectivamente, a tres personas y a cuatro personas, confirmando las respuestas que ha recibido la persona que ha hecho la pregunta.

Por lo tanto, la respuesta es que llegó en cuarto lugar.