Prueba de selección para ESTALMAT 2016 Se dirige a una edad de: 11/13
Disponemos de muchas cuentas, numeradas del 0 al 7.
Tratamos de hacer pulseras, siguiendo unas reglas.
En cada pulsera, al sumar los números de dos cuentas consecutivas, debe dar el número de la que les sigue.
Si esa suma es mayor de 7, empezaremos a contar desde 0 de nuevo, es decir, si la suma da once, por ejemplo, la cuenta que pondremos será la 3, ya que el ocho es como la cuenta 0, el nueve será como el 1, el diez como el 2, y el once como el 3. En el momento que vuelvan a repetirse dos cuentas, podremos cerrar la pulsera.
Un ejemplo de pulsera sería la que aparece debajo de esta línea.
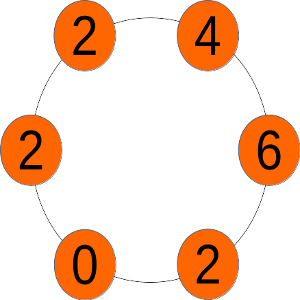
Indica todas las pulseras diferentes que pueden construirse, detallando por qué no pueden hacerse más.
Se trata de un problema de explorar y construir, que parece muy largo, pero no lo es tanto si nos fijamos un poco.
Como podríamos empezar por cualquier par de cuentas, imaginemos que empezamos por el par 1 – 1, por ejemplo. Tendríamos que poner a continuación el 2, el 3, el 5 y después el 0, el 5, el 5, el 2, el 7, el 1, el 0, el 1 y otra vez el 1. Como hemos repetido, cerramos una pulsera 1 – 1 – 2 – 3 – 5 – 0 – 5 – 5 – 2 – 7 – 1 – 0 . Esta pulsera tiene 12 cuentas, y empezando con cualquier par de ellas saldría la misma pulsera (es decir, si empezamos con las cuentas 1 – 2 o con las cuentas 0 – 5 también obtenemos la misma pulsera). Para construir una pulsera diferente hay que buscar un par que no esté en ninguna de las dos que ya conocemos. Ya tenemos una pulsera con 6 (la del ejemplo) y otra con 12.
La tercera pulsera la podemos empezar, por ejemplo, con las cuentas 1 – 3, ya que esta pareja no ha aparecido hasta ahora. Sale 1 – 3 – 4 – 7 – 3 – 2 – 5 – 7 – 4 – 3 – 7 – 2 , y también tiene 12 cuentas.
Con 1 – 4 sale la pulsera 1 – 4 – 5 – 1 – 6 – 7 – 5 – 4 – 1 – 5 – 6 – 3, también de 12.
Con la pareja 1 – 5 o la pareja 1 – 6 de nuevo sale la misma. La última que tiene 1 es 1 – 7 – 0 – 7 – 7 – 6 – 5 – 3 – 0 – 3 – 3 – 6.
Ya tenemos todos los pares que empiezan con 1. Con 2, tenemos ya el 2 – 0 (la de ejemplo), 2 – 1 (la segunda de las de 12, observa que acaba en 2 y empieza en 1) y, siguiendo así, sólo falta el 2 – 6, que da 2 – 6 – 0 – 6 – 6 – 4, de nuevo una pulsera de 6 cuentas.
Fíjate que las pulseras dependen de los pares de cuentas, pero también del orden. No sale la misma pulsera si empezamos con 1 – 2 que con 2 – 1. La siguiente cuenta sería la misma en los dos casos, pero la cuarta no, en un caso sale 1 – 2 – 3 – 5 y en el otro 2 – 1 – 3 – 4, es decir, que se construyen pulseras diferentes. Así que hay que revisar todos los pares, que serán 64 distintos.
Con 3, ya han salido todas las parejas, pero con 4 falta 4 – 0 – 4, una pulsera con sólo 3 cuentas.
Podemos revisar ahora todas las parejas que empiezan por 5, 6 o 7, pero las vamos a encontrar en las pulseras que llevamos encontradas.
He dejado para el final la más extraña, ya que si empezamos por 0 – 0, tenemos una pulsera de 2 cuentas, pero que, si pensamos bien, en realidad debería tener sólo una cuenta, ya que 0 es la siguiente a sí misma y también el resultado de la suma.
Además, si añadimos esta pulsera a la lista de pulseras, habremos utilizado en realidad 64 cuentas para hacer estas 8 pulseras (6 + 12 + 12 + 12 + 12 + 6 + 3 + 1 = 64), que coincide exactamente con todos los posibles pares que forman con ocho cuentas diferentes (8 diferentes para la primera y otras 8 para la segunda). Si las pones ordenadas, es sencillo verlo:
0-0, 0-1, 0-2, … , 0-7
1-0, 1-1, 1-2, … , 1-7
2-0, 2-1, 2-2, … , 2-7
…
7-0, 7-1, 7-2, … , 7-7
En realidad, esta última observación no sale de forma automática. Al principio, la pulsera con sólo un 0 la tenía con dos 0, y por tanto usaba 65 cuentas. Me llamó la atención, pero no relacioné lo que sucedía hasta que traté de hacer algo similar con otra cantidad de cuentas (en mi caso, probé a hacer pulseras sólo con las cuentas del 0 al 3, y me salía 0, 0 – 1 – 1 – 2 – 3 – 1, 0 – 2 – 2, y 0 – 3 – 3 – 2 – 1 – 3, que son en total 16 cuentas 1 + 6 + 3 + 6 = 16). Al ver una cantidad tan similar al cuadrado de 4 en un caso y al cuadrado de 8 en otro, le busqué una explicación.
Y es que cada pareja sale una única vez, y cada cuenta aparece (por ser circulares las pulseras) en dos parejas, con la de delante y con la de detrás. Por eso usamos las mismas cuentas que parejas.
La respuesta es, por tanto, que se pueden hacer 8 pulseras, que aparecen detalladas a continuación:
2 – 2 – 4 – 6 – 2 – 0
1 – 1 – 2 – 3 – 5 – 0 – 5 – 5 – 2 – 7 – 1 – 0
1 – 3 – 4 – 7 – 3 – 2 – 5 – 7 – 4 – 3 – 7 – 2
1 – 4 – 5 – 1 – 6 – 7 – 5 – 4 – 1 – 5 – 6 – 3
1 – 7 – 0 – 7 – 7 – 6 – 5 – 3 – 0 – 3 – 3 – 6
2 – 6 – 0 – 6 – 6 – 4
4 – 0 – 4
0