Fase Comarcal de la Olimpiada Matemática de la Comunidad Valenciana 2016, nivel B Se dirige a una edad de: 15/16
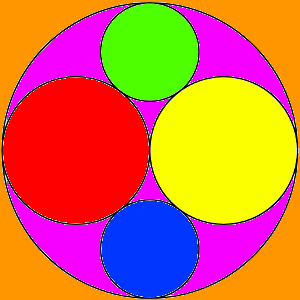
En el dibujo, podemos ver cinco circunferencias, una más grande que contiene a las otras, dos medianas y dos más pequeñas. Todas son tangentes a tres o cuatro de las otras.
Sabemos que el radio de las circunferencias medianas mide 1 metro. ¿Cuánto mide el radio de las pequeñas?
El primer paso para este tipo de problemas es trazar los radios de las circunferencias que llegan a los puntos de tangencia, para establecer relaciones entre ellas.
A veces, no es necesario usar todos los radios, e incluso conviene borrar lineas para ver triángulos interesantes. Muy frecuentemente, debemos buscar triángulos isósceles formados por los radios (uniendo también los puntos de tangencia entre ellos), o triángulos rectángulos.
Con todos estos segmentos dibujados, enseguida vemos varias relaciones, incluyendo un triángulo rectángulo que se dibuja dentro de las circunferencias. Sabemos que es rectángulo por la simetría de la figura.
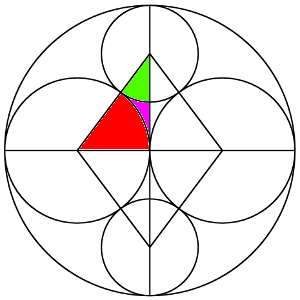
Observa que el radio de la grande medirá 2, claramente.
Y el triángulo rectángulo, suponiendo que r es el radio que buscamos (el de la circunferencia pequeña), tendrá los siguientes lados: la hipotenusa medirá 1 + r, un cateto medirá 1, y el otro medirá 2 – r.
Aplicando el Teorema de Pitágoras, tendremos que (1 + r)2 = 1 + (2 – r)2, y desarrollando la expresión, tenemos que 1 + 2r + r2 = 1 + 4 – 4r + r2, de donde tenemos que 6r = 4, por lo que el radio debe medir exactamente 2/3, es decir, 66,7 centímetros aproximadamente.