Primer nivel de la Olimpiada de Mayo, 2016.
Se dirige a una edad de: 12 años

A cada número de tres dígitos Matías le sumó el número que se obtiene invirtiendo sus dígitos.

Por ejemplo, al número 927 le sumó el 729.

Calcular en cuántos casos el resultado de la suma de Matías es un número con todos sus dígitos impares.

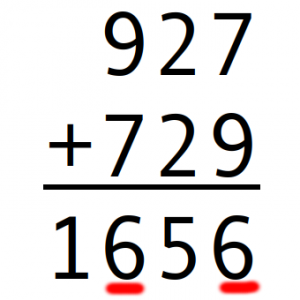
Solución:

Al invertir las cifras de un número de tres cifras, la segunda cifra coincide en ambas, de forma que la suma de ambas va a ser un número par.

Si queremos que todas las cifras sean impares, debemos entonces tener dos cifras en el último y primer puesto que sumen más de 9, para cambiar este hecho. Además, deben sumar impar.

Pueden sumar 11, 13, 15 o 17, ya que tienen que estar entre el 0 y el 9.

Pero, además, la segunda cifra, al sumarse consigo misma (duplicarse) no debe pasar de 8, porque si pasa, aporta una unidad más a la cifra de las centenas del resultado, y la volverá par (porque antes de eso debe ser la misma que la última).

Por tanto, las combinaciones de primera y última cifra son 2 – 9, 3 – 8, 4 – 7, 5 – 6, 4 – 9, 5 – 8, 6 – 7, 6 – 9, 7 – 8 y 8 – 9. Un total de 10 posibilidades, en cualquier orden (lo que hace 20).

Y, para la cifra central, tenemos las posibilidades: 0, 1, 2, 3 o 4, lo que hace 5.

Combinar estas dos situaciones se hace mediante la multiplicación, ya que para cada uno de los 20 casos de primera y última cifra, hay cinco posibilidades para la central.

Por tanto hay 100 situaciones que dan todas las cifras impares, evidentemente, 50 de ellas son las mismas, pero invertidas. Veamos algunos ejemplos

209 + 902 = 1111

219 + 912 = 1131

229 + 922 = 1151

239 + 932 = 1171

249 + 942 = 1191

308 + 803 = 1111

…

439 + 934 = 1373

…

849 + 948 = 1797