Canguro matemático (nivel 3) 2017
Se dirige a una edad de: 14 años

ABCD es un paralelogramo.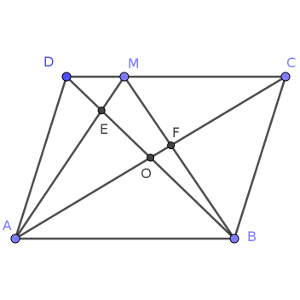

El punto O es la intersección de las diagonales del paralelogramo. El punto M está en el lado DC. El punto de intersección de BM y AC es F. La suma de las áreas de los triángulos AED y BFC es 1/3 del área S del paralelogramo.

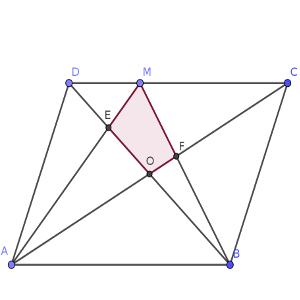
¿Cuánto vale el área del cuadrilátero EOFM, en función de S?

Puesto que el concurso es de respuesta cerrada, se nos ofrecían cuatro alternativas, S/6, S/8, S/10, S/12 y S/14.

Solución:

Este problema fue el más difícil del nivel 3 del curso pasado. En realidad, la dificultad reside en que cuesta mucho poner un ejemplo y empezar a trabajar sobre él, y que el tiempo del que disponemos es escaso en un concurso como éste, de velocidad.

La clave del problema consiste en descomponer el área total del cuadrilátero en piezas de la misma área, o que de alguna forma se puedan comparar.

Primero, visualicemos el área que se nos dice que es 1/3.

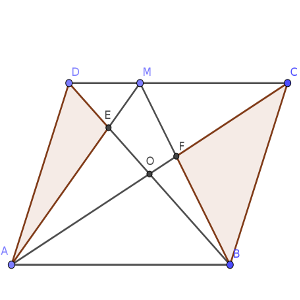
Destaca que nuestro objetivo forma parte del triángulo que ocupa la parte central, ABM, que remarcamos en nuestra segunda imagen.

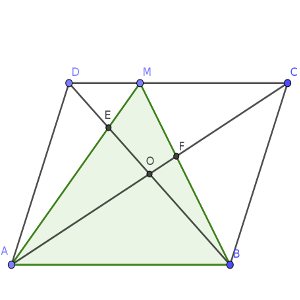
Es sencillo ver que este triángulo ABM tiene un área que es la mitad del paralelepípedo, ya que su base y su altura son idénticas. Por lo tanto, sumadas entre sí, ocuparían S/2 + S/3 = 3S/6 + 2S/6 = 5S/6.

Por lo tanto, la diferencia entre la suma de estas dos áreas y el total, serían el par de triángulos DEM y CFM, que tendrían una extensión de S/6. (ver tercera figura).

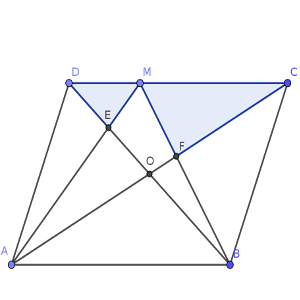
Pero el cuadrilátero EOFM que buscamos, unido a la pieza que tenemos, forma el triángulo DCO.

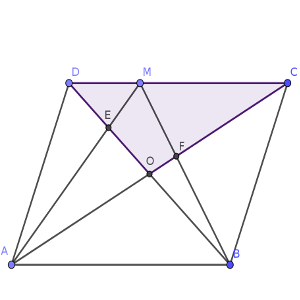
Y está claro que este triángulo ocupa la cuarta parte del paralelogramo. Por lo tanto, nuestro cuadrilátero tiene una extensión de S/4 – S/6 = 3S/12 – 2S/12 = S/12, que era la cuarta de las sugerencias.

Para terminar, se puede observar que se podría haber empezado por pensar en un área concreta (por ejemplo, 24 unidades, para poder proceder más rápido a sumar las fracciones.