Canguro matemático (nivel 6) 2017 Se dirige a una edad de: 17 años
Si |x| + x + y = 5 y x + |y| – y = 10 ¿cuál es el valor de x + y?
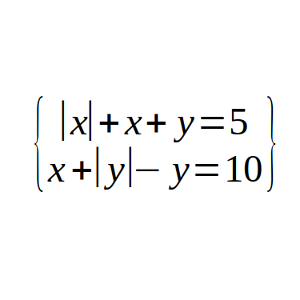
Solución:
El valor absoluto es un elemento sencillo de tratar, pero mucha gente se olvida de que puede cambiar el signo de las expresiones que contenga, en función de que sean positivas o negativas.
En el caso de este sistema, basta considerar cuatro casos, en los que las expresiones de las variables pueden ser positivas o negativas.
Incluso, si somos ordenados, podremos decidir la solución con sólo una elección de signo.
Supongamos que la x es positiva. En ese caso, la primera ecuación se convierte en 2x + y = 5, de forma que si en la segunda multiplicamos por 2, tendremos 2x + 2|y| – 2y = 20, así que si cambiamos de signo y restamos la primera expresión, tenemos 2|y| – 3y = 15. Evidentemente, la y debe ser negativa, ya que en caso contrario tendríamos con toda seguridad un número negativo en la primera parte de la igualdad, por lo que tendremos que – 5y = 15, y deducimos que y = – 3, y por tanto x = 4. La respuesta a la pregunta debe ser que x + y suma 1.
La respuesta ya la podríamos marcar, pero si quisiéramos cubrir todas las posibilidades, deberíamos contemplar también la opción de que la x pudiese ser negativa, pero en ese caso la primera ecuación quedaría – x + x + y = 5, y en ese caso la y valdría 5, pero en la segunda ecuación, si probamos ese valor para y, queda x = 10, lo que no puede suceder, puesto que x debería ser negativa.
Para un problema de velocidad como es éste, nunca debemos valorar la opción de elevar al cuadrado tras despejar para eliminar el valor absoluto, práctica muy habitual que en este caso (y en muchos otros) complica demasiado la expresión.