Solución a un par de ángulos

Canguro matemático (nivel 5) 2017
Se dirige a una edad de: 16 años

ABC es un triángulo. El punto D se elige de forma que DC = AB.

El punto M es el punto medio entre A y D, y el punto N es el punto medio entre B y C.

Si entendemos que el ángulo NMC es x, entonces, el ángulo BAC ¿qué vale, en función de x?

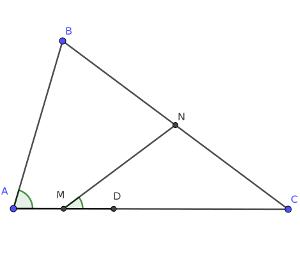
Puesto que el concurso es de respuesta cerrada, se nos ofrecían cinco alternativas:  2x, 90 – x, 45 + x, 90 – x/2, o 60º.
Solución:

Este problema fue el más difícil del nivel 5 del curso pasado. Puesto que se trata de un problema con opciones, la forma más rápida de contestar consiste en partir de un triángulo conocido y hacer el cálculo. Es muy rápido probar con un equilátero y medio cuadrado en dos posiciones, y ayuda a descartar todas las opciones menos una.

En efecto, en el equilátero tenemos que D coincide con A, y por simetría, x mide 30 y el otro ángulo mide 60, de forma que rápidamente tenemos que 45 + x y 90 – x/2 quedan descartadas. Si ponemos el medio cuadrado de forma que AC sea la diagonal, entonces repetimos la situación y x es 45 y el otro 90, con lo que descartamos 90 – x y 60. La otra posición nos puede servir para asegurarnos, pero la respuesta debe ser 2x.

Ahora, vamos a aprovechar que tenemos tiempo para confirmar que, en efecto, el otro ángulo es siempre 2x.

En esta ocasión tampoco encontramos una manera sencilla de acortar el proceso, aunque el hecho de que aparezcan un ángulo y su doble sugiere que debería poderse convertir en un ángulo central y uno inscrito, pero no parece fácil.

De nuevo utilizaremos fórmulas propias de la geometría algebraica, aunque no es sencillo. Recordamos que el coseno del ángulo entre dos vectores es el cociente entre su producto escalar y el producto de sus módulos. También necesitaremos la fórmula trigonométrica que relaciona el coseno de un ángulo con el coseno de su doble.

Para que salgan expresiones sin fracciones, tomaremos A como (0,0), B como (2x, 2y), y C como (2, 0) (esto siempre podemos lograrlo porque cualquier triángulo lo podemos fijar para que la unidad de medida sea la mitad del lado AC). Para facilitar el cálculo, tomaremos d como la mitad de la distancia entre A y B, es decir, que d = raíz(x² + y²).

El punto D, por tanto, será el punto (2 – 2d, 0) y el punto N será (x + 1, y). El punto M será (1 – d, 0). Necesitaremos más adelante el vector MN, que será el vector de componentes (x + d, y). Su módulo lo denominaremos v = raíz ((x + d)² +y²).

De el ángulo entre el vector AB y el vector AC, podemos calcular con facilidad su coseno, mediante la fórmula cos(p) = (2x, 2y)·(2,0)/(2*2d) = 4x /4d = x/d. La expresión no puede ser más sencilla.

Ahora bien, la expresión del coseno del ángulo entre MN y MC no es tan sencilla. Aquí, cos(q) = (x + d, y)·(1 + d, 0)/(v*(1+d)) = (x + d)(1 + d)/(v*(1 + d)) = (x + d)/v.

A partir de aquí, necesitamos conocer la relación entre un coseno de un ángulo y su doble. La relación debería ser que cos(p) = 2(cos(q))² – 1, por lo que trataremos de aplicar esa fórmula al cos(q) y simplificarlo hasta ver si queda cos(p).

Por lo tanto, tratemos de calcular 2(x + d)²/v² – 1 y ver si es equivalente a x/d.

Recordamos que v² = (x + d)² +y², por lo que 2(x + d)²/v² – 1 = (2(x² + 2xd + d²) – ((x + d)² +y²))/((x + d)² +y²) = (2x² + 4xd + 2d² – (x² + 2dx + d² +y²))/((x + d)² +y²) = (2x² + 4xd + 2d² – x² – 2dx – d² – y²))/((x + d)² +y²) = (x² + 2xd + d² – y²))/(x² + 2dx + d² +y²).

También sabemos que d² = x² + y² , de forma que donde esté al cuadrado podemos sustituir, quedando (x² + 2xd + d² – y²))/(x² + 2dx + d² +y²) = (x² + 2xd + x² + y² – y²))/(x² + 2dx + x² + y² +y²) = (2x² + 2xd))/(2x² + 2dx + 2y²) = (x² + xd))/(x² + dx + y²) = (x² + xd))/(d² + dx).

De esta última expresión, podemos sacar factores y queda (x² + xd))/(d² + dx) = (x·(x + d))/(d·(d + x)) = x/d.

Por lo tanto, tras mucho trabajo, conseguimos demostrar que el ángulo entre MN y NC es, en efecto, la mitad que el ángulo entre AB y AC.