Problema 0 de la Olitele (Olimpiada Telemática de Cataluña) 2017
Se dirige a una edad de: 16-17 años

Si escribiésemos el resultado de la operación 2015²⁰¹⁶ + 2016²⁰¹⁷ + 2017²⁰¹⁸ + 2018²⁰¹⁹ + 2019²⁰²⁰ con un único número entero ¿cuál sería la cifra de las unidades de ese número?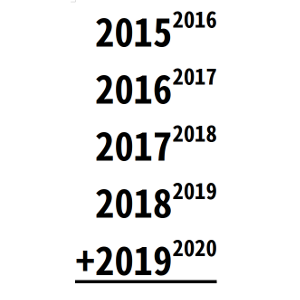
Solución:

No tenemos ninguna propiedad que nos permita sumar potencias, salvo un factor común, que en este caso no existe, pues todas las bases son diferentes.

De forma que, si necesitamos calcular el valor de este número, será necesario trabajar con todas sus cifras, que son más de 6600 (el logaritmo de 2019, multiplicado por 2020, supera esta cifra).

Pero como sólo necesitamos la última cifra, podemos molestarnos en calcular la última cifra de cada uno de los sumandos y deducirla de ahí. La última cifra de un producto sólo depende de las últimas cifras de cada uno de los factores, de forma que nos fijaremos en esos factores.

Puesto que 5·5 = 25, todas las potencias de números que acaban en 5, también acaban en 5, por lo que 2015²⁰¹⁶ acaba en 5.

De forma similar, puesto que 6·6 = 36, 2016²⁰¹⁷ acaba en 6.

Sin embargo, las demás potencias no son tan sencillas. La más simple es la que acaba en 9, ya que 9·9 = 81, es decir, el cuadrado de un número acabado en 9, acaba en 1. Y la última cifra del cubo de un número que acabe en 9, será 9 (ya que 9·1 = 9). Y, repitiendo la operación, la potencia cuarta acabará en uno, y la quinta en 9. Se trata de un ciclo de orden dos. En resumen, que cada potencia impar acabará en 9 y cada potencia par, en 1 (incluso la potencia en la que el exponente es cero). Por lo tanto 2019²⁰²⁰, acabará en 1.

Las potencias de números que acaban en 7 son algo más complicadas. El cuadrado acaba en 9 (7·7 = 49), el cubo acaba en 3 (9·7 = 63), la potencia cuarta acaba en 1 (3·7 =21) y vuelta a empezar en un ciclo de orden 4 (7 – 9 – 3 – 1). Cuando elevemos a un múltiplo de 4, tendremos un 1 como última cifra, y en este caso, puesto que 2016 es un múltiplo de 4, 2017²⁰¹⁶ acaba en 1, 2017²⁰¹⁷ acaba en 7 y 2017²⁰¹⁸, la que buscamos, acaba en 9.

Y nos quedan las que acaban en 8. El cuadrado acaba en 4 (8·8 = 64), el cubo en 2 (4·8 =32), la potencia cuarta en 6 (2·8 = 16) y la potencia quinta vuelve a acabar en 8 (6·8 = 48). Es decir, el ciclo de nuevo es cuatro (8 – 4 – 2 – 6). La única diferencia con 7 es que la potencia de exponente 0 no está en el ciclo (en el caso del 7 sí lo está). Pero en este caso, todas las potencias múltiplos de 4 mayores que cero acaban en un 6, de forma que 2018²⁰¹⁶ acaba en 6, 2018²⁰¹⁷ acaba en 8, 2018²⁰¹⁸ acaba en 4, y 2018²⁰¹⁹ la que buscamos, acaba en 2.

Como las últimas cifras de los cinco sumandos son, respectivamente, 5, 6, 9, 2 y 1, la última cifra de la suma será la misma que la de 5 + 6 + 9 + 2 + 1 = 23, es decir, que la suma que buscamos acabará en 3.