Problema 1 de la Olitele (Olimpiada Telemática de Cataluña) 2017
Se dirige a una edad de: 16-17 años

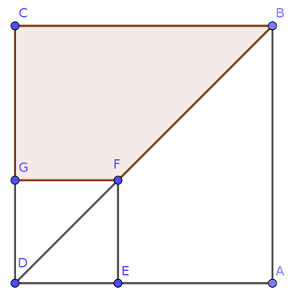
En la figura, ABCD y EFGD son cuadrados.

Si conocemos la longitud de BF, que llamamos d, y el área de BCGF, que llamamos S, calcula el área del cuadrado ABCD.

Solución:

La estrategia pasa por relacionar d, S y el área del cuadrado de alguna forma, y calcular a partir de esa relación el área del cuadrado, que es lo que buscamos.

Para lograrlo, es más sencillo trabajar en principio con el lado del cuadrado, AB, ya que es un recurso al que estamos más acostumbrados. Llamemos x a este valor.

El área del triángulo BCD será x²/2, y el triángulo FGD es semejante. Si encontramos su relación de semejanza, podremos calcular su área. Restando esas dos cantidades, encontraremos S, y por tanto una relación.

La longitud de la diagonal DB es x·raíz(2) (aplicando el Teorema de Pitágoras, o por proporcionalidad con el cuadrado de lado 1). Puesto que BF vale d, DF vale x·raíz(2) – d.

La proporción entre BCD y FGD (factor de escala) será, por tanto, x·raíz(2)/(x·raíz(2) – d). Sobre el área debemos aplicarla al cuadrado, así que para calcular el área de FGD debemos dividir x²/2 entre el cuadrado del factor de escala.

El área de FGD será, por tanto, (x²/2):(x·raíz(2)/(x·raíz(2) – d))² = (x²·(x·raíz(2) – d)²)/(4·x²) = (x·raíz(2) – d)²/4.

De esa expresión, tenemos que S = x²/2 – (x·raíz(2) – d)²/4. Reduciendo a común denominador y desarrollando el cuadrado de la resta, tenemos que S = 2x²/4 – (x·raíz(2) – d)²/4 = (2x² – 2x² + 2dx·raíz(2) – d²)/4 = (2dx·raíz(2) – d²)/4.

De la fórmula que hemos conseguido, S = (2dx·raíz(2) – d²)/4, podemos despejar ahora la x, ya que 4S = 2dx·raíz(2) – d², por lo que 4S + d² = 2dx·raíz(2). Por último, dividiendo ambos extremos por el factor que multiplica la x, tenemos que (4S + d²)/(2d·raíz(2)) = x, que es la expresión que buscamos.

Bueno, en realidad el área será esa expresión al cuadrado, es decir, A = (4S + d²)²/(8d²)