Problema 2 de la Olitele (Olimpiada Telemática de Cataluña) 2017 Se dirige a una edad de: 16-17 años
Disponemos de 21 puntos, de forma que hay 11 en una recta y 11 en otra (uno de ellos está en la intersección).
¿Cuántos triángulos podemos trazar cuyos vértices sean tres de esos puntos?
Si los tres puntos están sobre la misma recta se considera que no pueden formar un triángulo.
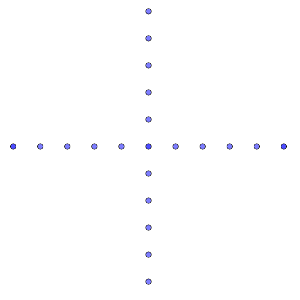
Solución:
Es de mucha utilidad tratar de hacer el recuento en un conjunto de puntos en dos rectas mucho más pequeño, por ejemplo, 5 puntos repartidos en dos rectas.
Tenemos dos aproximaciones. En un caso, tratar de contar los conjuntos de tres puntos con la condición geométrica de que formen un triángulo, o la otra manera de trabajar es contarlas todas y descontar aquellos conjuntos que estén sobre la misma recta.
En la primera aproximación, puesto que queremos que formen un triángulo, contaremos por separado los casos en que contenga el punto de intersección y los que no.
En cualquier caso, puesto que hay dos rectas, necesitamos que dos puntos estén en una recta, y otro en otra.
De los que no contienen el de intersección, tenemos 10·9/2 = 45 formas de escoger un par de puntos de una recta (10 formas de elegir el primero y 9 del segundo, pero como podemos elegirlos en un orden o en otro, dividimos por 2) y 10 formas de elegir el otro, por lo que tenemos 450 triángulos con dos puntos en una recta y uno en otra. Puesto que podríamos tener una cantidad idéntica cambiando de recta, tenemos un total de 900 triángulos.
Si contiene la intersección, debemos elegir un punto en cada una de las dos rectas, es decir, que tendremos 10·10 = 100 formas de elegirlos.
En total, 900 + 100 = 1000 triángulos diferentes.
Si utilizamos la otra aproximación, hay que contar cuántos conjuntos de tres puntos diferentes podemos hacer, y descontar los alineados.
El número total de conjuntos de tres puntos sería 21·20·19/(3·2) = 7·10·19 = 1330.
La cantidad de conjuntos de tres puntos alineados sobre una de las rectas sería 11·10·9/(3·2) = 11·5·3 = 165, pero como son dos rectas habrá un total de 165 + 165 = 330 conjuntos alineados, lo que deja un total de 1330 – 330 = 1000 triángulos diferentes con esas condiciones.