Problema 2 del viernes de la Fase Local de la Olimpiada Matemática Española 2018 Se dirige a una edad de: 16-17 años
¿De cuántas maneras se puede escribir 111 como suma de tres números enteros en progresión geométrica?
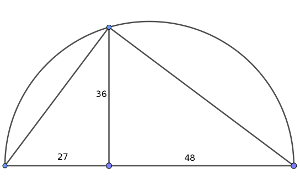
En la imagen vemos tres números enteros, en este caso positivos, que forman una progresión geométrica (con representación geométrica, además). Recordad que una progresión geométrica es aquella en la que, a partir del segundo término, cada uno de ellos es igual al anterior por una cantidad constante.
Solución:
¡Atención! Se trata de un problema muy largo, según yo lo veo.
Este problema, de apariencia sencilla, supuso un reto importante para todos los participantes, ya que era fácil dejar escapar alguna posibilidad.
Algebraicamente, tres números en progresión geométrica serían a, x·a y x²·a. Por lo tanto, la identidad que pretendemos resolver es 111 = a + ax + ax², pero encontrar sólo las soluciones en las que a, x·a y x²·a sean números enteros, positivos o negativos. Sin embargo, x puede ser un número entero o bien un número racional. No podría ser, por ejemplo, irracional, ya que xa debe ser entero.
Es evidente que se puede factorizar como 111 = a(1 + x + x²), y a partir de ahí, la solución oficial opta por transformar el segundo factor en p/q y trabajar con las diferentes posibilidades de p y q.
Me pareció más intuitivo tratar de resolver a partir del entero a el valor de x, razonando que podíamos convertir en una ecuación de segundo grado la igualdad anterior, algo como ax² + ax + a – 111 = 0, de forma que en ese caso, x = (-a+raíz(a² – 4·a·(a – 111)))/2a, donde tenemos dos soluciones según el signo de la raíz.
Eso quiere decir que el contenido de la raíz debe poder ser un cuadrado perfecto, ya que de no ser así, x sería irracional, por lo que la expresión a² – 4·a·(a – 111) es un cuadrado perfecto. Eso limita mucho los valores de a. Esa expresión, quitando paréntesis, se transforma en a² – 4·a² +444a = 444a – 3a², que es una expresión de segundo grado.
Es fácil saber cuándo esa expresión alcanza su valor mínimo, en cero, en los casos en que a vale 0 o bien a vale 148 (444/3), y en ambos casos tenemos valores válidos para nuestra x. Pero al ser de segundo grado, su valor más alto lo alcanza en el punto medio, en 74, en el que alcanza un valor de 16428. Este es un valor muy alto para ir probando uno por uno, así que debemos sacar factores comunes. Aunque a es un factor común en la expresión, no conocemos mucho de él, de forma que no es conveniente. Rápidamente, encontramos el valor 3, que es un factor común. Como es un cuadrado perfecto, deberíamos poder sacar dos factores 3, de forma que la expresión (148a – a²)/3 debe ser entero y un cuadrado perfecto. Eso deja el valor más alto posible en 1825, aproximadamente, que está próximo al cuadrado de 42. Esto es más razonable, y podemos tantear usando esos 42 cuadrados.
Para tantear más cómodo, supondremos la igualdad (148a – a²)/3 = n² para cada uno de ellos, de donde sacamos el valor de a. Quitando denominadores, tenemos que 148a – a² = 3n², por lo que 0 = 3n² – 148a + a², y por tanto a = (148 + raíz(21904 – 12n²)) / 2.
Analizamos ahora los diferentes valores. Podemos dividir la expresión entre 2 para hacer más fácil la prueba, ya que también saldrá un cuadrado, claro. Así, a = 74 + raíz(5476 – 3n²) La expresión con la que he probado es con 5476 – 3n², poniendo una tabla de cuadrados hasta el 73 (conviene preparar una tabla con los cuadrados, es muy sencillo hacerlo a mano, sumando cada vez un impar, y a la vista de la fórmula, también los triples).
Si n vale 0, la raíz da 74, y tenemos que a puede valer 148 o bien cero, con lo que x vale -1/2 en el primer caso, y no se puede calcular (no sirve como progresión que sume 111) en el segundo. Primera progresión, 148, -74 y 37.
Si n vale 1 no sale un cuadrado. Tampoco para 2, ni para 3, 4, 5, o 6.
Sin embargo, para 7 sí funciona, vemos que 5476 – 3·49 es el cuadrado de 73. Eso nos lleva a que a = 147, y usando esa información, calcular x como -3/7, lo que da unos enteros como 147, -63 y 27.
Con el mismo valor de a = 147, podemos obtener un valor de x de -4/7, lo que nos lleva en ese caso a 147, -84 y 48.
Para el mismo valor de n = 7, tenemos que a puede valer también 1, con lo que en ese caso tenemos que x puede valer 10, y tendríamos 1, 10 y 111.
Y si a = 1, otro valor posible para la x es -11, lo que lleva a 1, -11 y 121.
Sigamos variando la n, tenemos que no vuelve a salir bien (en algunos casos por muy poco) hasta que la n vale 33, en el que 5476 – 3n² es el cuadrado de 47. De nuevo, la a puede valer dos cosas. Si a vale 121, la x puede valer -1/11, con lo que tenemos 121, -11 y 1.
Con la a = 121, también puede ser que x valga -10/11, y tendríamos 121, -110 y 100.
Y si la a = 27, tenemos el valor de x = 4/3, que da 27, 36 y 48.
También para la a = 27, tenemos que x = -7/3, y da 27, -63 y 147.
El siguiente valor de n para el que esa raíz da entera es 37, y en ese caso, el valor de la raíz es precisamente 37.
En ese caso, la a puede valer 111, y la x puede valer 0, así que tendríamos 111, 0 y 0.
También para a = 111, x = -1, y entonces tendríamos 111, -111 y 111.
Con esa misma n = 37, a puede valer 37, y en ese caso x puede valer 1. Da 37, 37 y 37.
Si a = 37, por último, x puede valer -2, teniendo 37, -74, 148.
Seguimos probando valores de n, y llegamos a n = 40. En ese caso, la raíz da 26. y la a puede ser 100. En ese caso, x puede valer 1/10, y tenemos 100, 10 y 1.
Con a = 100, también puede ser x = -11/10, y tenemos 100, -110 y 121.
Pero con el mismo valor de n también a puede ser 48, y en ese caso, la x puede valer 3/4, con lo que tendríamos 48, 36 y 27.
Y para a = 48, tenemos que x puede ser -7/4, que proporciona 48, -84 y 147.
Y para 41 y 42 no da ningún cuadrado, de forma que estas son todas las posibilidades que hay, ya que para valores superiores la raíz da negativa.
Las fórmulas que he usado, en resumen, sería, partiendo de n, y la tabla de cuadrados, calcular 5476 – n² y ver si está en la tabla, anotas la raíz entera r. Calculas luego a como 74 + r o bien como 74 – r. Y por último, sacas x como (-a + 3n)/(2a) o bien como (-a – 3n)/(2a). Cada valor de n, excepto el primero, da lugar a cuatro posibilidades.
Hay un total de 17 diferentes casos. En realidad, muchas de ellos están compuestas de los mismos números, ya que empezamos por delante o por detrás. Sólo 111, 0, 0, 37, 37, 37 y 111, -111, 111 no se repiten. Si las contamos así, se reducen a 10 casos.
Sugiero leer también la solución oficial, que omite ciertos casos, que yo creo que también habría que comparar a mano, pero que parece más breve que la mía.
Tabla de cuadrados (la dificultad de hacer este cálculo a mano es evidente, las diferencias las hago para calcular rápido y corregir posibles errores):
| Valores | Cuadrados | Diferencia | Triples | Diferencias | Resta de 5476 |
| 0 | 0 | 1 | 0 | 3 | 5476 |
| 1 | 1 | 3 | 3 | 9 | 5473 |
| 2 | 4 | 5 | 12 | 15 | 5464 |
| 3 | 9 | 7 | 27 | 21 | 5449 |
| 4 | 16 | 9 | 48 | 27 | 5428 |
| 5 | 25 | 11 | 75 | 33 | 5401 |
| 6 | 36 | 13 | 108 | 39 | 5368 |
| 7 | 49 | 15 | 147 | 45 | 5329 |
| 8 | 64 | 17 | 192 | 51 | 5284 |
| 9 | 81 | 19 | 243 | 57 | 5233 |
| 10 | 100 | 21 | 300 | 63 | 5176 |
| 11 | 121 | 23 | 363 | 69 | 5113 |
| 12 | 144 | 25 | 432 | 75 | 5044 |
| 13 | 169 | 27 | 507 | 81 | 4969 |
| 14 | 196 | 29 | 588 | 87 | 4888 |
| 15 | 225 | 31 | 675 | 93 | 4801 |
| 16 | 256 | 33 | 768 | 99 | 4708 |
| 17 | 289 | 35 | 867 | 105 | 4609 |
| 18 | 324 | 37 | 972 | 111 | 4504 |
| 19 | 361 | 39 | 1083 | 117 | 4393 |
| 20 | 400 | 41 | 1200 | 123 | 4276 |
| 21 | 441 | 43 | 1323 | 129 | 4153 |
| 22 | 484 | 45 | 1452 | 135 | 4024 |
| 23 | 529 | 47 | 1587 | 141 | 3889 |
| 24 | 576 | 49 | 1728 | 147 | 3748 |
| 25 | 625 | 51 | 1875 | 153 | 3601 |
| 26 | 676 | 53 | 2028 | 159 | 3448 |
| 27 | 729 | 55 | 2187 | 165 | 3289 |
| 28 | 784 | 57 | 2352 | 171 | 3124 |
| 29 | 841 | 59 | 2523 | 177 | 2953 |
| 30 | 900 | 61 | 2700 | 183 | 2776 |
| 31 | 961 | 63 | 2883 | 189 | 2593 |
| 32 | 1024 | 65 | 3072 | 195 | 2404 |
| 33 | 1089 | 67 | 3267 | 201 | 2209 |
| 34 | 1156 | 69 | 3468 | 207 | 2008 |
| 35 | 1225 | 71 | 3675 | 213 | 1801 |
| 36 | 1296 | 73 | 3888 | 219 | 1588 |
| 37 | 1369 | 75 | 4107 | 225 | 1369 |
| 38 | 1444 | 77 | 4332 | 231 | 1144 |
| 39 | 1521 | 79 | 4563 | 237 | 913 |
| 40 | 1600 | 81 | 4800 | 243 | 676 |
| 41 | 1681 | 83 | 5043 | 249 | 433 |
| 42 | 1764 | 85 | 5292 | 255 | 184 |
| 43 | 1849 | 87 | 5547 | -71 | |
| 44 | 1936 | 89 | |||
| 45 | 2025 | 91 | |||
| 46 | 2116 | 93 | |||
| 47 | 2209 | 95 | |||
| 48 | 2304 | 97 | |||
| 49 | 2401 | 99 | |||
| 50 | 2500 | 101 | |||
| 51 | 2601 | 103 | |||
| 52 | 2704 | 105 | |||
| 53 | 2809 | 107 | |||
| 54 | 2916 | 109 | |||
| 55 | 3025 | 111 | |||
| 56 | 3136 | 113 | |||
| 57 | 3249 | 115 | |||
| 58 | 3364 | 117 | |||
| 59 | 3481 | 119 | |||
| 60 | 3600 | 121 | |||
| 61 | 3721 | 123 | |||
| 62 | 3844 | 125 | |||
| 63 | 3969 | 127 | |||
| 64 | 4096 | 129 | |||
| 65 | 4225 | 131 | |||
| 66 | 4356 | 133 | |||
| 67 | 4489 | 135 | |||
| 68 | 4624 | 137 | |||
| 69 | 4761 | 139 | |||
| 70 | 4900 | 141 | |||
| 71 | 5041 | 143 | |||
| 72 | 5184 | 145 | |||
| 73 | 5329 | 147 | |||
| 74 | 5476 | 149 | |||
| 75 | 5625 | 151 | |||
| 76 | 5776 | 153 | |||
| 77 | 5929 |
gracias