Problema 5 de la Olitele (Olimpiada Telemática de Cataluña) 2017 Se dirige a una edad de: 16-17 años
Una sucesión an se define de la siguiente manera: a1 = 4, a2 = 6 y an+1 = an/an-1 para valores de n mayores o iguales que 1.
Encuentra el valor de la suma de los términos a2016 + a2017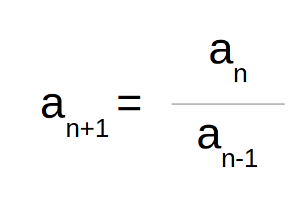 .
.
Solución
Este problema es realmente sencillo. Lo primero que debemos hacer es buscar un patrón en la sucesión recursiva que nos permita calcular valores avanzados, porque tratar de calcular una fórmula general para el cociente de dos consecutivos no ofrece buenas soluciones.
La sucesión, en sus primeros términos sería 4, 6, 6/4, 1/4, 1/6, 4/6, 4, 6, …
Tal y como leemos la fórmula, vemos que cada término sólo depende de los dos anteriores, por lo que en cuanto se repiten dos, se inicia un ciclo. Es decir, que la sucesión en realidad es cíclica y se repite exactamente igual cada 6 términos. Así, los términos de posición múltiplo de seis valdrán todos lo mismo, es decir, 4/6 = 2/3, mientras que el siguiente valdrá 4, y así sucesivamente.
Lo único que tenemos que hacer es averiguar qué parte del ciclo ocupa el término de posición 2016 y el 2017. Puesto que 2016 es divisible entre 6, está claro que serán el 2/3 y el 4, así que su suma será 14/3.