Problema 6 de la Olitele (Olimpiada Telemática de Cataluña) 2017 Se dirige a una edad de: 16-17 años
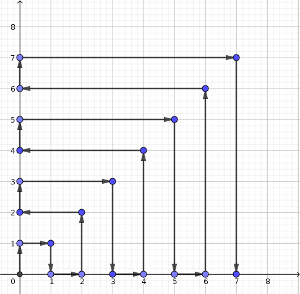
Un robot circula por un plano coordenado de la forma que marca el dibujo.
Así, tras llegar al punto (7, 0), avanzará una unidad en horizontal hasta el (8, 0), subirá en vertical 8 unidades hasta el (8, 8) y retrocederá en horizontal ocho unidades hasta el (0, 8), y así sucesivamente.
Si cada unidad del plano mide un centímetro, ¿en qué coordenadas se encontrará cuando haya recorrido exactamente 2017 centímetros?
Solución:
Parte del dibujo puede recordar la suma de una progresión aritmética, o tal vez un cuadrado. Y es por ahí por donde vamos a empezar, descubrir un patrón que cada cierto tiempo pueda darnos una progresión y poder calcular de vez en cuando sumas, de forma sencilla, hasta encontrar qué vuelta estará dando cuando llegue a 2017 centímetros.
Podemos fijarnos, por ejemplo, en los momentos en los que llega al eje horizontal, o en los que sale (total, la diferencia es de 1), o en los que llega al eje vertical (o en los que sale). Para concretar, vamos a empezar por los momentos en los que llega al eje vertical, en los que el siguiente movimiento es subir una unidad vertical.
La primera vez que pasa, ha recorrido 0. La segunda vez (que llega al (0, 2)), ha recorrido nada menos que 8 centímetros. La tercera vez (llega al (0, 4)), ha recorrido 16 más, lo que hace un total de 24. La cuarta vez (llega al (0, 6)), habrá recorrido 24 más, lo que hace un total de 48.
Lo que parece ser una progresión aritmética es la cantidad de centímetros recorridos desde una vez a otra (0, 8, 16, 24), que empieza por 0 y tiene una diferencia de 8. Vamos a comprobarlo.
Supongamos que es cierto hasta un valor n. Habrá llegado, según hemos visto, hasta la posición (0, 2n – 2). Recorrerá una unidad hacia arriba, hasta el (0, 2n – 1), y, después, 2n – 1 unidades a la derecha hasta la posición (2n – 1, 2n – 1). Otras 2n – 1 unidades hacia abajo hasta el (2n – 1, 0), una más a la derecha ((2n, 0)) y 2n arriba y 2n a la izquierda, lo que le lleva al (2n, 2n) y al (0, 2n). En total, habrá recorrido 1 + 2n – 1 + 2n – 1 + 1 + 2n + 2n = 8n, que es exactamente lo que predice la progresión aritmética (0 + 8·(n + 1 – 1)) para la posición n + 1. y que llega a la posición (0, 2·(n + 1) – 2), que es realmente el (0, 2n). De esta forma, por inducción, hemos comprobado que sí pasa de esta forma.
Vale, ahora sabemos que para cada vez que llegue al eje vertical habrá sumado los términos de la progresión hasta ese momento, que sabemos que para n términos será (0 + 8·(n – 1))·n /2 = 8·(n – 1)·n/2 = 4·n·(n – 1). Si hubiésemos optado por otra posición, la fórmula podría haber cambiado ligeramente.
Ahora tenemos que ver cuando ese valor está cerca de 2017, que es como si resolviésemos una ecuación, pero igual no da exacto, nos quedaremos con el valor entero más próximo por debajo.
Si 4·n·(n – 1) = 2017, tenemos la ecuación 4n² – 4n = 2017, es decir, 4n² – 4n – 2017 = 0. Aplicando la fórmula de la ecuación de segundo grado (la variante positiva, que la negativa da números negativos que no tienen sentido aquí), tenemos que n = (4 + raíz(16 + 4·4·2017))/8. Podemos sacar factor común 16 de los elementos de la raíz, y eso facilita los cálculos, ya que es igual que 4 + 4·raíz(1 + 2017))/8 = (1 + raíz(2018))/2. Podemos ver que la raíz de 2018 está por debajo de 45, por lo que el último n válido será (1 + 43)/2 = 22.
Para ese valor (cuando llegue a la posición (0, 42)) habrá recorrido 4·22·21, que da 1848 centímetros recorridos. Después, subirá uno hacia arriba (1849) al (0, 43), se moverá 43 a la derecha (1892) al (43, 43), bajará 43 (1935) al (0, 43), se moverá uno a la derecha (1936) al (0, 44), 44 hacia arriba (1980) al (44, 44). Si se mueve 44 a la izquierda, sumaría más de 2017, por lo que sólo se puede mover 37 a la izquierda y en ese momento estará en la posición (7, 44), que es la respuesta correcta.
Seguramente habría sido mucho más sencillo tomar un valor de n una unidad mayor y “retroceder” a la búsqueda de la posición adecuada.
Gracias por compartir este bonito problema para fomentar la divulgación en matemáticas.
Solución alternativa
———————————-
Si nos fijamos después de moverse 4=2² veces está en la posición (2,0); despues de moverse 9=3² veces está en la posición (0,3)….
2017=44²+81… pues vamos a movernos… (44,0) y toca subir 44 … nos quedan 37 para 81 (81-44)… pues desde el (44,44) nos movemos 37 en horizontal posicionándonos en (7,44) que es la SOLUCIÓN FINAL.
Espero que os guste el atajo.