Problema 8 de la Olitele (Olimpiada Telemática de Cataluña) 2017
Se dirige a una edad de: 16-17 años

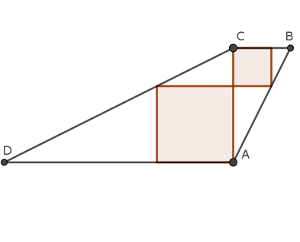
En un cuadrilátero como el de la figura, con dos lados paralelos, encajamos dos cuadrados diferentes, con un lado en cada uno de los lados paralelos. Un vértice de cada cuadrado coincide con uno de dos de los vértices opuestos del trapecio, y otro de los vértices de ambos cuadrados coinciden entre sí.

Conocemos la longitud de la diagonal del trapecio AC (que coincide con los lados de los cuadrados), y el área del trapecio. Se pide calcular la suma del área de ambos cuadrados.

Solución

Es evidente que el espacio en blanco corresponde a cuatro triángulos rectángulos, que son semejantes.

Es facil verlo, ya que dos de ellos tienen exactamente los mismos catetos (los dos lados de los cuadrados), por lo que son iguales, y los otros dos tienen lados paralelos a los que son iguales, con lo que son claramente semejantes. Para facilitar los cálculos, vamos a llamar x e y a los lados de los cuadrados. Para aclararnos, x en el dibujo es el lado del grande, que comparte vértice con el punto A, mientras que y es el cuadrado del pequeño, el que tiene un vértice en C.

Los datos que tenemos son S, el área del trapecio, y p, que sería la longitud AC. Lo que queremos es determinar de alguna manera la suma de las áreas de los dos cuadrados, que llamaremos T.

De momento, la primera tarea es relacionar esos tres datos con x e y, las longitudes de los lados de los cuadrados.

Es evidente que T=x² + y². Y que p = x + y. Para hallar el área del trapecio ABCD, podemos usar la fórmula del área del trapecio, pero suele ser mejor idea descomponerlo en figuras más sencillas (para eso usamos el dibujo) y sumar esas áreas. Ya tenemos los dos cuadrados. Los triángulos rectángulos medianos que son iguales tienen dos catetos que valen x e y, de forma que su área es x·y/2 cada uno, es decir, entre ambos suman x·y.

El triángulo que tiene un vértice en D es semejante al que tiene un vértice en C, su cateto menor en la imagen mide x, mientras que el cateto menor del que tiene el vértice C es y. Por tanto, la escala entre ambos es x/y (si multiplicas y por x/y obtienes x). Como el cateto grande del triángulo en C mide x, tenemos que el cateto grande del que tiene el vértice en D será x·x/y = x²/y., por lo que su área será x³/(2y). Razonando de manera similar, el área del otro triángulo será y³/(2x), por lo que la igualdad será S = x² + y² +xy + x³/(2y) + y³/(2x).

Ahora que tenemos las tres igualdades, se trata de eliminar de llas las variables x e y, utilizando álgebra.

T = x² + y²
p = x + y
S = x² + y² + xy + x³/(2y) + y³/(2x)

Si ŕeducimos a común denominador en la expresión tercera, tenemos que 2xyS/(2xy) = 2x³y/(2xy) + 2y³x/(2xy) + 2x²y²/(2xy) + x⁴/(2xy) + y⁴/(2xy). Quitando denominadores y ordenando por el grado en x, por ejemplo, tenemos la expresión 2xyS = x⁴ + 2x³y + 2x²y² + 2y³x + y⁴.

Esta última expresión recuerda un poco a la potencia cuarta de x + y, que sería (x + y)⁴ = x⁴ + 4x³y + 6x²y² + 4y³x + y⁴. Si añadimos y restamos lo que necesitamos, tendríamos que 2xyS = (x + y)⁴ – (2x³y + 4x²y² + 2y³x), con lo que la expresión pierde el término más grande. Hay que tener en cuenta que x + y = p, así que en realidad la potencia cuarta ya no depende de x e y realmente.

Otro paso sería sacar factor común del contenido de paréntesis, y quedaría 2xyS = (x + y)⁴ – 2xy(x² + 2xy + y²) y por tanto lo del dentro del paréntesis es exactamente el cuadrado de la suma, de forma que 2xyS = (x + y)⁴ – 2xy(x + y)² = p⁴ – 2xyp².

Recapacitemos:
T = x² + y²
p = x + y
2xyS = p⁴ – 2xyp²

El factor 2xy ha aparecido para que podamos convertir la larga expresión de x e y en algo relacionado con p. Podemos hacer algo similar con T, ya que x² + y² = (x + y)² – 2xy, por lo que T = p² – 2xy. Si usamos la igualdad con T y la igualdad con S para despejar y sustituir 2xy, podemos lograr una expresión sin x ni y.

T = p² – 2xy lleva a que 2xy = p² – T, por lo que la expresión queda (p² – T)S = p⁴ – (p² – T)p² = p⁴ – p⁴ – Tp² = – Tp² .

Como lo que tenemos que calcular es T, basta despejarla de la igualdad, de forma que (p² – T)S = -Tp² lleva a Sp² – TS + Tp² = 0 por lo que Sp² = TS – Tp² = T(S – p²), y así se da que T = Sp²/(S – p²).

Esta fórmula (T = Sp²/(S – p²)) es la que buscamos.