Problema 10 de la Olitele (Olimpiada Telemática de Cataluña) 2017
Se dirige a una edad de: 16-17 años

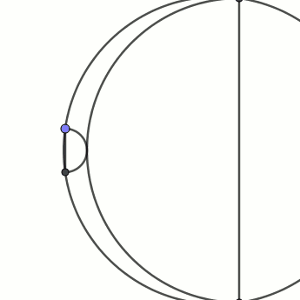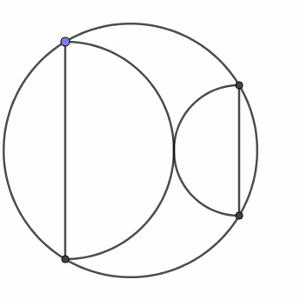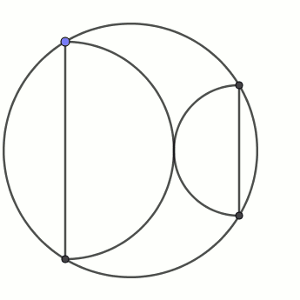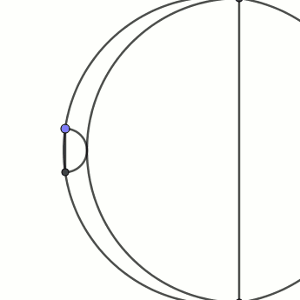
En el interior de una circunferencia dibujamos dos semicircunferencias tangentes entre sí de forma que los diámetros son paralelos y tienen los extremos en puntos de la circunferencia.

Demuestra que la suma de las áreas de las dos semicircunferencias es exactamente la mitad del área del círculo de la circunferencia inicial.

Solución:

Puesto que los radios de las semicircunferencias son perpendiculares a la tangente, ambos radios estarían sobre la misma recta. Si los continuamos hasta que corten a la circunferencia, tendremos dos puntos de corte que formarán, por la simetría de la figura, un diámetro. Llamemos p y q a los segmentos que las prolongan y x e y los radios de las semicircunferencias. Supongamos que p está junto a y y q junto a x.

El dibujo queda como sigue.

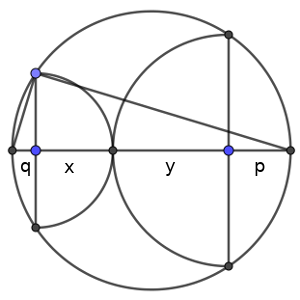
Puesto que los puntos extremos de las semicircunferencias están sobre la circunferencia, son vértices de triángulos rectángulos cuya hipotenusa es el diámetro de la circunferencia original, y su alturas miden lo mismo que los radios x e y.

Un triángulo rectángulo apoyado sobre la hipotenusa es dividido por la altura en dos triángulos rectángulos semejantes con él mismo, razonando por igualdad de ángulos, y por tanto semejantes entre sí. De ahí se deduce el teorema de la altura, aunque eso no imprescindible que lo conozcas.

Lo importante es que el triángulo rectángulo formado por el segmento p como cateto horizontal y el radio y como vertical, es semejante al formado por el cateto y como vertical y el cateto y + x + q como horizontal, de forma que p/y = y/(x + y + q).

De forma similar, con el otro punto en la circunferencia, logramos probar que q/x = x/(x + y + p).

Eliminando en ambas igualdades los denominadores, queda px + py + pq = y², y la otra queda qx + qy + qp = x². Si despejamos en una de ellas (por ejemplo, en la primera, la q) y sustituimos en la otra, podemos encontrar una relación entre p, x e y.

Así, pq = y² – px – py, por lo que q = y²/p – x – y. Al sustituir en la segunda, tenemos que (y²/p – x – y)x + (y²/p – x – y)y + (y²/p – x – y)p = x². Quitamos paréntesis, y tenemos xy²/p – x² – xy + y³/p – xy – y² +y² – xp – yp = x².

Eliminando términos, llegamos a que xy²/p – 2x² – 2xy + y³/p – xp – yp = 0. Ahora, quitamos denominadores multiplicando por p, llegando a xy² – 2x²p – 2xyp + y³ – xp² – yp² = 0.

La última expresión que hemos obtenido recuerda un poco a una ecuación de segundo grado cuya incógnita sea p, podemos ordenarla un poco y clarificar los coeficientes: – xp² – yp² – 2x²p – 2xyp + xy² + y³ = 0. Es decir, -(x + y)p² – 2x(x + y)p + y²(x + y) = 0. Está claro que el factor x + y está presente en todos los términos y podemos simplificar la ecuación, pues no vale cero. Cambiando el signo, queda p² + 2xp – y² = 0. De esa igualdad, aplicando la ecuación de segundo grado (o cuadrando por productos notables), llegamos a que p = (-2x + raíz(4x² + 4y²))/2 = -x + raíz(x² + y²). Evidentemente, la opción negativa no tiene sentido en este problema.

Trabajando exactamente igual con la q, o bien sustituyendo este valor en la ecuación situada dos párrafos más arriba, tenemos que q = -y + raíz(x² + y²).

Ahora, sumando los cuatro segmentos, el diámetro de la circunferencia, que vale dos veces el radio, será 2r = p + x + y + q = -x + raíz(x² + y²) + x + y – y + raíz(x² + y²) = 2·raíz(x² + y²), por lo que r = raíz(x² + y²).

De esta forma, el área del círculo exterior, Pi·r² = Pi·(x² + y²) = Pi·x² + Pi·y², que sería la suma de las áreas de las circunferencias pequeñas completas, es decir, el doble de la suma de las áreas de las semicircunferencias que propone el problema.