Problema 4 de la Fase Local (viernes) de la Olimpiada Matemática Española (2018) Se dirige a una edad de: 16-17 años
Determina los números reales x > 1 para los cuales existe un triángulo cuyos lados tienen las longitudes siguientes:
x⁴ + x³ + 2x² + x + 1
2x³ + x² + 2x + 1
x⁴ – 1.
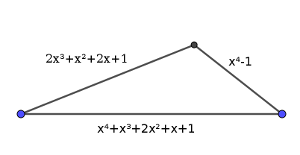
Solución: Aquí
Los lados son
a=x^4+x^3+2x^2+x+1=(x^2+1)(x^2+x+1)
b=2x^3+x^2+2x+1=(x^2+1)(2x+1)
c= x^4-1=(x^2+1)(x^2-1)
Los tres lados son mayores que 0 para x>1.
El lado a es el mayor de los tres lados cuando x>1.
Además, si x>1, se cumple que a>b+c. Entonces siempre es posible construir un triángulo con dichos lados (desigualdad triangular).
Errata: el signo de la desigualdad es incorrecto. Debe ser “a x^2+x+1 (para x>1)