Problema 4 de la Fase Local (viernes) de la Olimpiada Matemática Española (2018)
Se dirige a una edad de: 16-17 años

Determina los números reales x > 1 para los cuales existe un triángulo cuyos lados tienen las longitudes siguientes:

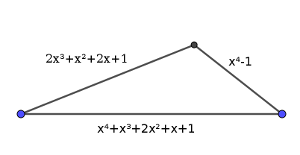
x⁴ + x³ + 2x² + x + 1

2x³ + x² + 2x + 1

x⁴ – 1.

Solución:

Para que se pueda construir un triángulo de ese tipo, se debe cumplir que los tres números sean positivos, y que el mayor de los tres sea menor que la suma de los otros dos. Si no queremos comparar las tres cantidades para ver cuál de las tres es la mayor (porque además, podría variar con el valor de x), podemos tratar de ver que ninguna de las tres sea mayor que la suma de las otras dos.

Puesto que x es mayor que 1, está claro que los dos primeros son positivos, ya que están compuesto de sumas de potencias de x. Y el tercero sólo le quita 1 a una potencia de 1, con lo que también lo es. Por lo tanto esa característica está verificada.

Ahora, si queremos que a + b > c, es equivalente a comprobar que a + b – c es mayor que cero.

Si sumamos los dos primeros y restamos el tercero, tenemos el polinomio 3x³ + 3x² + 3x + 3, que claramente es positivo para todos los valores de x positivos.

Si sumamos el primero y el tercero, y restamos el segundo, tenemos el polinomio 2x⁴ – x³ + x² – x – 1. Como tiene restas, deberemos ver qué raíces tiene para estudiar su signo mediante la factorización (convertirlo en un producto). Probando a dividirlo por x – 1, da exacto, de forma que el polinomio se podría poner como (x – 1)·(2x³ + x² + 2x + 1). Y está claro que ambos polinomios son positivos, el primero por ser la x mayor que 1 y el segundo por ser una suma de números positivos. Luego esa suma siempre es mayor que el otro lado.

Por último, si sumamos el segundo y el tercero, y restamos el primero, tendremos el polinomio x³ – x² + x – 1, que de nuevo podemos factorizar dividiendo por x – 1, obteniendo este polinomio como (x – 1)·(x² + 1), que por idénticas razones es positivo.

Como conclusión, podemos encontrar ese triángulo para cualquier x mayor que 1.