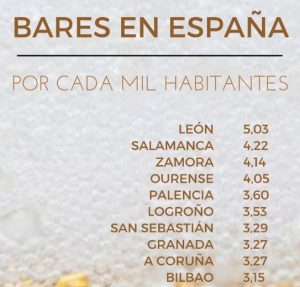
España es un país de bares. Lo sé, esto no va a sorprenderle. En junio de 2017, el número de bares en España ascendía a 101397, es decir, 2.8 bares o cafeterías por cada 1000 habitantes. Quizás le sorprenda más saber que las capitales con más bares por habitante no son ni Granada, ni Sevilla, ni siquiera Madrid, sino León, Salamanca y Zamora (ver, por ejemplo, este enlace).

Por otra parte, España ha pasado a los octavos de final del mundial de Rusia gracias al VAR (video assistant referee, por si no lo sabía) y, lo sé, esto tampoco le va a sorprender. En este sentido, el VAR consiste en una serie de cámaras que deben servir para reducir la incertidumbre en el arbitraje de un partido de fútbol).

Sin embargo, el VaR, así con uve, y en mayúsculas y minúsculas, siglas de Value at Risk (en inglés) o Valor en Riesgo (en español), es una noción matemática de suma importancia, por ejemplo, en finanzas que ya existía mucho antes del mundial de Rusia y que persigue, de alguna manera, el control de la incertidumbre, expresada como un riesgo.

El término riesgo tiene muchas acepciones dependiendo de la persona y del contexto en el que nos refiramos a él. El riesgo de no estudiar para un examen es suspenderlo, el riesgo de hacer una escape room es no salir de ella, el riesgo de hacer una entrada dentro del área es que te piten penalti y el riesgo de comprar una papeleta de lotería es perder el dinero que nos costó. En general, y hablando muy coloquialmente, podríamos coincidir en que el riesgo es la posibilidad (o no) de experimentar ciertos eventos de interés y las consecuencias derivadas de ellos (que no tienen por qué ser negativas, oiga).

Fijemos una situación desde un punto de vista bien sencillo: piense el lector que dispone de un activo financiero A que puede reportarle beneficios (o pérdidas, que es lo que más “debería” interesarnos). Si yo le digo que el VaR (value at risk, valor en riesgo) de dicha inversión A (al 95%, por defecto) es de 100 euros, debe entender que 100 euros es la máxima pérdida que usted sufrirá el 95% de las ocasiones durante cierto periodo de tiempo. También podríamos pensar que sólo el 5% de las ocasiones perderemos más de 100 euros.

Suponga ahora que yo, como inversor prestigiosísimo, le propongo una inversión B cuyo VaR (de nuevo, al 95%) es de 50 euros o, lo que es lo mismo, si usted me lo compra el 95% de las ocasiones sufrirá una pérdida menor de 50 euros ¿qué activo financiero preferiría: A ó B? No es aventurado pensar que la mayoría de ustedes preferirían B. Además, si se lo digo yo, que soy gran conocedor de las finanzas…

Y la respuesta es que sí: es cierto que, a priori, podríamos estar de acuerdo, que todos dispondríamos de la inversión B en nuestra “cartera” y que todos esperaríamos obtener muchos beneficios o, al menos, perder menos que aquéllos propietarios de la inversión A.

Si bien es cierto que inversores de todo el mundo llevan años preocupados por medir el posible riesgo existente a la hora de adquirir una cartera, no fue hasta finales de 1980 cuando surgió el concepto de VaR que acabamos de comentar. En 1987, y después de una fuerte crisis financiera, Dennis Weatherstone (presidente de la compañía financiera estadounidense JP Morgan & Co.) tomó la decisión de solicitar un informe breve y diario donde se plasmase el riesgo de pérdida en cartera durante las siguientes 24 horas y este fue el origen del uso del VaR como medida de riesgo. Esta medida cobró tal importancia a lo largo de los años que terminó por convertirse en la herramienta más utilizada a nivel mundial para medir el posible riesgo a la hora de invertir en una determinada cartera. De hecho, el Comité de Supervisión Bancaria de Basilea, es decir, la organización mundial que reúne a las autoridades de supervisión bancaria a fin de fortalecer la solidez de los sistemas financieros y reducir el riesgo, y que se reúne periódicamente, estableció en origen un VaR al 95% como medida de riesgo preferente y, en 1995, aumentó el nivel al 99%, es decir, querían controlar no el 95% de las ocasiones, sino el 99%.

Desde el punto de vista matemático, si X es una variable aleatoria que expresa los beneficios o pérdidas de una inversión el VaR no es más que la función cuantil evaluada en cierta probabilidad p=0.95 ó p=0.99. No se agobie, si usted es madre o padre, seguro que ha usado la función cuantil anteriormente. Si le dicen que su hijo, que tiene 5 semanas y pesa 4.8 kg, está en el percentil 72.6, seguramente se quedará tranquilo, porque esto querrá decir que el peso de su bebé es mayor que el peso de aproximadamente el 73% de los niños de su edad (ver la siguiente figura, http://www.percentilesinfantiles.es/). Evidentemente, esto ha sido calculado a partir de los pesos registrados de miles y miles de bebés de su edad y es una buena señal del crecimiento. Los 99 posibles percentiles no son más que algunos (pocos) casos particulares de los infinitos cuantiles.

Hasta aquí todo, más o menos, bien, pero volvamos a nuestra inversión porque no es oro todo lo que reluce. Decíamos que si el VaR al 95% es igual a 100 euros, “esperaremos” no superar los 100 euros de pérdida en el 95% de las ocasiones, pero no se deje engañar: ¿qué ocurre el 5% restante? ¿Y si, por cosas del destino, una de esas veces ocurre que perdemos un millón de euros? Piénselo, algunos caminos son inexcrutables y hablar de probabilidades es simplemente eso: hablar de probabilidades.

Pero… realmente ¿puede ocurrir que perdamos un millón de euros cuando sabemos lo que ocurre el 95% de las veces? Pues ¡vaya que sí! Y si no que se lo digan a los gurúes de Wall Street o a nuestros amigos de JP Morgan. ¿Recuerdan la crisis que comenzó en 2008? Si todo estaba controlado (y bien controlado) por nuestro querido VaR, ¿cómo fue posible aquel batacazo económico mundial del que 12 años después aún no nos hemos recuperado?

Sea como fuere, se perdió de vista que lo único que mide el VaR es una probabilidad. Más concretamente, en tal caso hay un 99% de probabilidades de “no perder”, pero nadie miró a ese 1% restante hasta que finalmente sucedió y las pérdidas se acumularon en miles de millones, dando como resultado un efecto dominó que, sumado a la ineficacia, ineficiencia e ignorancia de los políticos, ya sabemos lo que provocó.

Ante tal catástrofe, el Comité de Basilea publicó en 2010 una revisión de los criterios oficiales para el control del riesgo promoviendo un cambio hacia otra medida de riesgo que sí tiene en cuenta el peso de las mayores pérdidas. Pero ojo, no cometamos de nuevo el error de pensar que lo que tiene probabilidades bajas de suceder, no sucederá.

Así que estimado lector o lectora, no hay nada como el calor del amor en un bar y tampoco hay nada que un VAR en el último minuto no arregle, pero nada como un VaR bien controladito para poder ir ver a España ganar el mundial de Rusia con un buen gin tonic entre las manos.

Escrito por Julio Mulero

Este post forma parte del Carnaval de Matemáticas, que en esta septuagésima octava edición, también denominada 9.2, está organizado por @Pedrodanielpg a través de su blog A todo Gauss.