Problema 1 del reto de selección para el MathCamp de Estados Unidos y Canadá (2018) Se dirige a una edad de: 14-17 años
João y Kinga juegan a un juego con un dado justo de n caras, que están numeradas del 1 al n. En este juego, a João se le asigna un valor j y a Kinga un valor k, ambos en rango del 1 al n. João y Kinga se turnan lanzando el dado, empezando a lanzarlo João.
Si João obtiene un número menor o igual que j, el juego acaba y él gana. Si Kinga obtiene un número menor o igual que k, entonces gana Kinga y el juego acaba. El juego continúa hasta que uno de los dos jugadores gana.
Demuestra que si j = k, entonces João siempre tiene ventaja.
Si n = 6, encuentra todos los posibles valores de j y k que hacen el juego justo (es decir, que hacen que tanto João como Kinga tengan una probabilidad de un 50% de ganar).
Si n = 101, demuestra que ningún valor de j y k hacen el juego justo.
Solución:
Primero, vamos a intentar entender cómo se calcula la probabilidad en un juego como éste con un ejemplo sencillo. En segundo lugar, trataremos de estudiar los tres casos propuestos.
Supongamos que el dado tiene sólo tres caras, que João usa un valor 1 y Kinga un valor 2.
Empieza jugando João, y la probabilidad de que en esa jugada el juego acabe, y João gane en ese caso es de 1/3.
En segundo lugar (si el juego no ha acabado, con una probabilidad 2/3), tira Kinga, y tiene una probabilidad de 2/3 de que el juego acabe y Kinga gane. Ésto se dará con una probabilidad 4/9.
Si ninguno de esos escenarios se da (lo cual sucederá con una probabilidad 2/9), volvemos a empezar el juego, que se desarrolla de la misma forma.
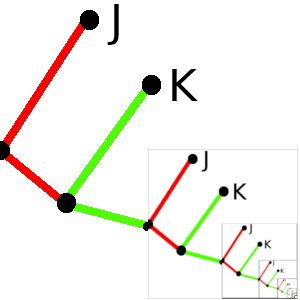
Hasta este punto, se trata de un cálculo de probabilidad en forma de árbol de dos bifurcaciones muy sencillo, pero a partir de este momento, se inicia un árbol infinito, que está ilustrado en la imagen y que no hace fácil el cálculo de las ocasiones en las que gana João, y las que gana Kinga. Lo que parece claro es que, puesto que la probabilidad de que siga sin acabar el juego después de dos jugadas se multiplica por 2/9, la probabilidad de que el juego siga indefinidamente tiende a cero, es decir, la probabilidad de que el juego acabe es 1.
Una forma de calcular la probabilidad que corresponde a João sería sumar la probabilidad de que gane en la primera tirada, más la de que gane en la tercera, más la de que gane en la quinta, y así sucesivamente en una suma infinita. Si nos damos cuenta, será sumar 1/3 + 2/9·1/3 + (2/9)²·1/3 +… ¿Reconocéis el patrón? En efecto, es una suma de una progresión geométrica. Se puede hacer a la manera telescópica, o bien con una fórmula, y su probabilidad será 1/3/(1 – 2/9) = 1/3·(9/7) = 3/7. Y, claro, la probabilidad de que sea Kinga la que gane, será 4/7 (calculada de la misma forma o bien restando de 1).
Otra forma es mediante una sencilla ecuación, pensando que si x es la probabilidad de que gane João, volverá a ser la probabilidad de que gane João si llegamos a la tercera jugada, por lo que x = 1/3 + 2/9·x, de donde obtenemos que x = 3/7, y de ahí la probabilidad de que gane Kinga será 4/7.
Una tercera forma es suponer que el caso en el que el juego continúa, no influye en el resultado del juego, es decir, los dos casos válidos suceden cantidades de veces equivalentes a 1/3 = 3/9 y 4/9, es decir, que la totalidad de resultados válidos son 7/9. Si repartimos la probabilidad entre ambo casos, respectivamente, tendremos (3/9)/(7/9) = 3/7 para João y (4/9)/(7/9)= 4/7 para Kinga.
Como vemos, las tres interpretaciones dan idéntico resultado. Podemos calcular las probabilidades con cualquiera de los tres métodos.
Vamos entonces con el apartado (a), en el que j = k = a. La probabilidad de que gane João en la primera jugada será a/n, y la probabilidad de que pasemos a la segunda jugada será (n – a)/n.
La probabilidad de que gane Kinga en esa segunda jugada será de a(n – a)/n² y la probabilidad de que lleguemos a la tercera jugada será de (n – a)²/n².
De nuevo, tratando el caso como en el ejemplo, la suma que hay que hacer para descubrir la probabilidad de João valdrá (a/n)/(1 – (n – a)²/n²) = (an²)/(2an² – a²n) = n/(2n – a), mientras que la probabilidad de que gane Kinga es 1 – n/(2n – a) = (n – a)/(2n – a). Evidentemente, puesto que a es un número entre 1 y n, la probabilidad no puede ser la misma nunca para ambos.
Vayamos con el apartado (b), en el que n vale exactamente 6, y debemos determinar j y k, en el supuesto de que ambas probabilidades valen un 50%.
En este caso, la probabilidad de que gane João en la primera jugada es j/6, mientras que la probabilidad de que lleguemos a la tercera jugada será (6 – j)·(6 – k)/36 = (36 – 6j – 6k + jk)/36.
De esta forma, la suma que lleva a la probabilidad de João es (j/6)/(1 – (6 – j)·(6 – k)/36) = 6j/(6j + 6k – jk). Puesto que esta probabilidad debe ser 1/2, la relación que se debe dar es que 12j = 6j + 6k – jk, de donde podemos deducir que 6j = k(6 – j), por lo que k = 6j/(6 – j) debe ser entero y estar entre 1 y 6. Puesto que j debe ser un valor entero entre 1 y 6, es sencillo estudiar cuáles cumplen esta condición. Para j = 1 no obtenemos un k entero, pero para j = 2, obtenemos un k = 3, y para j = 3, k = 6. No hay más valores, ya que k no puede superar el valor 6.
Como conclusión, para un dado de 6 caras el juego será justo (de forma muy evidente) si João juega con un valor 3 y Kinga con un valor 6 (en ese caso, seguro que el juego se acaba en menos de tres jugadas), y (de una forma más difícil de calcular, pero más interesante) si João juega con un 2 y Kinga con un 3.
Y, por último, vayamos con el apartado (c). Ahora, n = 101. La probabilidad de que João gane en la primera jugada será de j/101, y la de que llegue a la tercera jugada será de (101 – j)·(101 – k)/101².
De esta forma, la suma que lleva a la probabilidad de João es (j/101)/(1 – (101 – j)·(101 – k)/101²) = 101j/(101j + 101k – jk). Si queremos que esta probabilidad sea de 1/2, debe darse que 202j = 101j + 101k – jk, y por tanto 101j = k(101 – j). De esta relación, puesto que 101 es primo, y no puede dividir a 101 – j, que es necesariamente un número menor que 101, debe dividir a k, por lo que k debería ser 101, pero en ese caso, j debe valer la mitad de 101, que no es un número entero.
Por este motivo, no puede existir un juego justo de este tipo con un dado de 101 caras.