Problema 2 del segundo nivel de la Olimpiada de Mayo (2018) Se dirige a una edad de: 14 años
En un tablero 4×4 están escritos los números del 1 al 16, uno en cada casilla.
Andrés y Pablo eligen cuatro números cada uno.
Andrés elige el mayor de cada fila, y Pablo el mayor de cada columna.
Un mismo número puede ser elegido por ambos.
Luego, se eliminan del tablero todos los números elegidos.
¿Cuál es el mayor valor que puede tener la suma de todos los números que quedan en el tablero?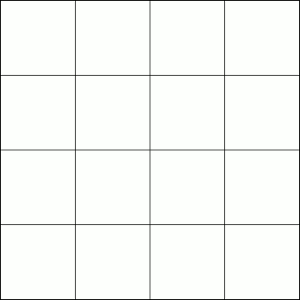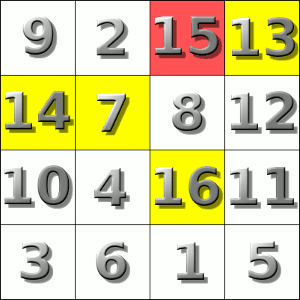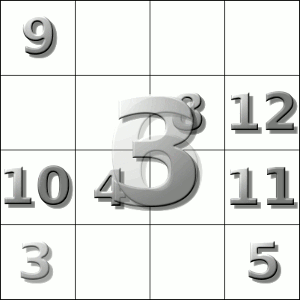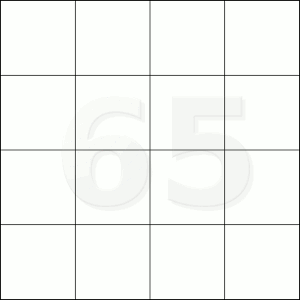
Si pensamos en lo que se nos propone, es lo mismo intentar que la suma de los que quedan sea lo mayor posible, que intentar que la suma de los que quitas sea lo menor posible, así que vamos a abordarlo por ese lado.
Veamos primero un ejemplo, distribuyendo al azar los 16 números y viendo lo que sucede.

Está claro que alguno de los números que ambos marcarán será el 16, y por lo tanto no elegirán 8 números, si no a lo sumo 7.
Uno de los dos elegirá el 15, ya que aunque esté en la misma fila que el 16, no puede estar también en la misma columna, por lo que el 15 será elegido. Sería buena idea que lo eligiesen los dos, ya que evitamos que elijan uno de los otros valores. Ahora bien, el 14 y el 13, si elegimos bien su posición (misma fila y columna que el 15 y el 16, podremos evitar que sean escogidos. De nuevo, es inevitable que el 12 lo escojamos, por lo que podemos tratar de que lo elijan ambos, y eso puede tapar una buena cantidad de números (11, 10, 9 y 8). De nuevo, el 7 lo elegiremos (mejor si son los dos), y así tenemos la cantidad más baja posible, que sería 16 + 15 + 12 + 7 = 50.
Un ejemplo de esa tabla sería la siguiente distribución de números, lograda alterando un poco el ejemplo anterior.

Ahora, hay que ver que nuestra intuición funciona, y que no hay una distribución mejor.
La clave es que, si suponemos que tenemos seleccionados los números que marcan los dos amigos de nuestro problema, podemos determinar el tamaño mínimo de los cuatro números más grandes, y ya sólo esos deben sumar más de 50.
Veamos. El mayor, claramente, es el 16. El segundo mayor es el 15, ya que o bien no está en la misma fila o en la misma columna que el 16.
Después, el tercero no puede estar en los dos cuadrados que están en la misma fila y columna en la que están el 15 y el 16. Hay 16 – 4 = 12 números fuera de esta condición, y claramente el mayor de todos será elegido, por uno o por otro, y será mayor o igual que 12.
Añadirá otra fila u otra columna, en la que no se podrá elegir ninguno. En el peor caso, quedará una fila o una columna en la que estará el cuarto, que no será ninguno de los dos anteriores. Por lo tanto, el mayor de esa fila o bien el mayor de la columna será el más grande de los dos, y será mayor que los 6 números restantes (los tres de su misma fila o columna, y los cuatro de la otra, aunque debe coincidir que un valor está en ambas), por lo que valdrá al menos 7.
Por lo tanto, los cuatro números mayores serán, con toda seguridad, mayores o iguales que 16, 15, 12 y 7, por lo que la suma total será al menos tan grande como el valor que hemos calculado previamente, 50.
Lo que pregunta el problema es cuánto suman los que quedan, y como en total siempre sumará lo mismo, basta restarle 50, o sumar los números restantes.
Para sumar los números del 1 al 16 (además de usar la conocida fórmula), podemos aplicar la estrategia de ir sumando por pares (1 + 16, 2 + 15, etc.) que nos da 8 pares que suman 17, luego la suma de los 16 sería 17*8 = 136.
Luego la suma de los que quedan será, en el caso mayor, 136 – 50 = 86 (podemos comprobarlo en el segundo ejemplo propuesto).
Para terminar, te dejo la encuesta para que evalúes la dificultad del problema.
[polldaddy poll=10107872]