Problema 4 del segundo nivel de la Olimpiada de Mayo (2018) Se dirige a una edad de: 14 años
En un paralelogramo ABCD, sea M el punto del lado BC tal que MC = 2BM y sea N el punto del lado CD tal que NC = 2DN.
Si la distancia del punto B a la recta AM es 3, calcular la distancia del punto N a la recta AM.
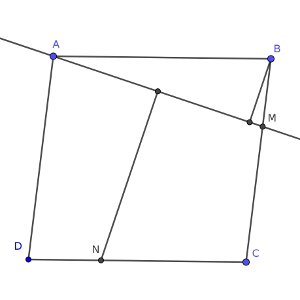
Solución:
Una de las formas de afrontar el problema, si aún no has visto coordenadas y te es difícil trabajar con variables (un alumno que tenga soltura con estos temas, tal vez pueda indicar la situación con ecuaciones de distancia, de recta y vectores), sería tratar de hacer triángulos semejantes, ya que cuentas con proporciones y ciertos ángulos.
Supongamos que los puntos donde mides las distancias de AM a B y de AM a N se llaman F y E, respectivamente.
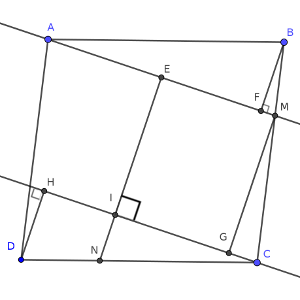
El triángulo BFM es rectángulo, y, como la distancia BM es la mitad de la distancia CM, podemos construir un triángulo rectángulo MGC semejante a BFM, pero de escala doble. Por eso, MG mide 6 unidades.
También podemos dibujar la recta paralela a AM, que corta al segmento EN en I. Es evidente, por ser perpendiculares a las rectas las distancias, que EMGI es un rectángulo, y que EI mide, por tanto, también 6.
Situemos ahora el segmento DH, perpendicular a AM, que hace que el dibujo sea tremendamente simétrico.
Pero CHD es evidentemente el mismo triángulo que ABF, por lo que DH mide 3. De nuevo por semejanza entre CHD y CIN, podemos saber que IN mide 2.
Y concluimos que EN mide 6 + 2 = 8.