Problema 6 del viernes de la Fase Local de la LV OME 2019
Se dirige a una edad de: 16-17 años

Fijamos un número natural k mayor o igual que 1. Encuentra todos los polinomios P(x) que cumplan P(x^k) – P(kx) = x^kP(x).

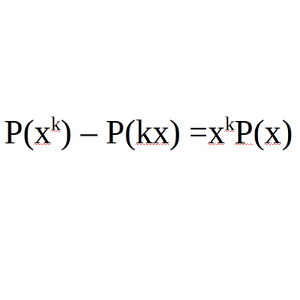
Solución:

En estos casos, siempre es conveniente experimentar un poco con los valores pequeños.

Si k = 1, la igualdad queda P(x) – P(x) = xP(x)., para cualquier x.

Claro, que como 0 = xP(x), el único polinomio que cumple esto es la constante 0. Es decir, P(x) = 0.

Claro que esa solución es válida para cualquier k, con lo cual, tenemos al menos una solución independiente de k, y para k = 1 no existen más.

Veamos qué pasa con k = 2. P(x²) – P(2x) = x²P(x).

Supongamos, por ejemplo, que es un polinomio de grado 1, de la forma ax + b. La igualdad queda ax² + b – ax – b = x²(ax + b) , por lo que ax² – ax = ax³ + bx². De nuevo, se tiene que dar para todo valor de x, de forma que a debe valer 0, porque no hay términos de tercer grado (o de primero) al otro lado de la igualdad, y b también.

Probemos ahora con un polinomio de grado 2: P(x) = ax² + bx + c, luego ax⁴ + bx² + c – 4ax² – 2bx – c = ax⁴ + bx³ + cx². De aquí, tenemos que bx² – 4ax² – 2bx= bx³ + cx², por lo que b debe valer 0 (mirando los términos de tercer grado), pero mirando los términos de segundo grado c = -4a, de forma que valen los polinomios de la forma ax² – 4a = a(x² – 4).

Veamos a continuación que si probamos con los polinomios de mayor grado, encontramos que se anulan todos los coeficientes.

Observa con ax³ + bx² + cx + d, en la igualdad queda un único término x⁶, con coeficiente a, luego a debe valer 0. Y como los polinomios menores ya sabemos lo que les pasa, sólo tenemos las dos soluciones encontradas ahora.

Supongamos que el grado del polinomio es n, mayor que 3 y que sabemos que no hay más soluciones para n – 1. Por inducción, si a es el coeficiente de grado n, ax²ⁿ sólo aparece en un extremo de la igualdad, en el otro el término de mayor grado es ax^{n + 2}, y 2n es mayor que n + 2, por ser n mayor que 3. Luego a vale 0, por lo que las únicas soluciones para k = 2 son las descritas.

Vale, ahora veamos qué sucede para valores de k mayores. En k = 3, la igualdad queda (por ejemplo, para segundo grado, fijándonos en el término mayor) ax⁶ = 0, por lo que el coeficiente del término de segundo grado es 0. Y para primer grado, queda ax⁴ = 0 (fijándonos en el término de la segunda parte de la igualdad). Los polinomios constantes ocasionan en la igualdad que el término de segundo grado sea ax² = 0, es decir, que no puede haber soluciones (más allá de la trivial, P(x) = 0) de grado menor que 2.

Veamos, por inducción, que tampoco puede haber soluciones de grado mayor para k = 3. Si no hay soluciones de grado n, supongamos que tenemos un polinomio de grado n + 1 y coeficiente principal a. La igualdad que debe cumplir transforma el grado, y su término mayor en la primera parte de la igualdad será ax^{3n + 3}, mientras que en la segunda será ax^{3 + n + 1}. Si se trata de grados diferentes, eso supone que a = 0. Si son iguales, entonces 3n + 3 = 3 + n + 1, por lo que 3n = n + 1, lo cual es imposible, ya que implicaría que 2n = 1.

Y esta situación ya nos permite trabajar para k genérico. Supongamos que k es mayor que 3. Para grado 1, por ejemplo, la primera parte de la igualdad tendría un término principal de ax^k, mientras que la segunda parte tendría un término de ax^{k + 1}, por lo que implicaría que el término principal de primer grado del polinomio se anularía. Y si el polinomio fuese constante, la primera parte de la igualdad se anula totalmente, de forma que sólo puede darse que el polinomio sea P(x) = 0.

Y, para polinomios de grados mayores que 1, supongamos que no existen polinomios de grado n que cumplen la igualdad, y veamos que tampoco existen de grado n + 1.

Si el grado es n + 1, el término de mayor grado de la primera parte de la igualdad sería ax^{kn + k}, mientras que el de grado mayor de la segunda parte sería ax^{k + n + 1}, y si uno es mayor que otro, entonces a = 0, y no existen por tanto polinomios de grado n + 1. Pero tampoco pueden ser del mismo grado, porque en ese caso kn + k = k + n + 1, es decir, kn – n = 1, con lo que (k – 1)n = 1, lo cual es imposible pues n es entero y k – 1 es mayor que 2.
En conclusión, si k no vale 2, sólo hay un polinomio que verifique la igualdad, P(x) = 0.

Si k vale exactamente 2, entonces P(x) = a(x² – 4), para cualquier valor de a (lo que incluye el caso en que a vale 0).