Problema 2 del sábado de la Fase Local de la LV OME 2019 Se dirige a una edad de: 16-17 años
Prueba que para todo a, b, c > 0 se cumple la siguiente desigualdad: a²/(b³c) – a/b² ≥ c/b – c²/a.
¿En qué caso se cumple la igualdad?
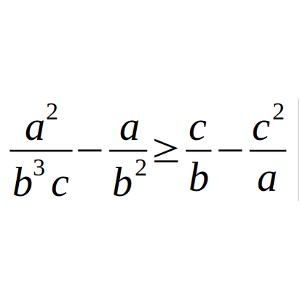Solución:
En esta ocasión se trata de un problema eminentemente algebraico, en el que un tratamiento sencillo de factorización nos da una respuesta de forma relativamente breve.
En otras desigualdades es imprescindible utilizar desigualdades que se conozcan previamente, como la desigualdad de las medias o cosas así, pero en esta ocasión no es imprescindible.
Básicamente, consiste en reducir todas las fracciones a un mismo denominador, ab³c, de forma que la desigualdad es equivalente a (a³)/(ab³c) – (a²bc)/(ab³c) >= (ab²c²)/(ab³c) – (b³c³)/(ab³c).
Puesto que el número ab³c es positivo, multiplicar ambos números por él mantiene la desigualdad, de forma que esta desigualdad es equivalente a a³ – a²bc >= ab²c² – b³c³.
Ahora bien, si sumamos o restamos la misma cantidad a dos valores, también mantienen la desigualdad que tengan, de forma que esta expresión es equivalente a a³ – a²bc – ab²c² + b³c³ >= 0.
Para factorizar esa expresión, podemos extraer el factor a² a los dos primeros sumandos, y b²c² a los dos siguientes, de forma que queda la desigualdad a²(a – bc) + b²c²(-a + bc) >= 0.
Si nos fijamos bien, las expresiones a – bc y -a + bc en realidad son opuestas, de forma que podemos extraer estas expresiones factor común, así que quedaría (a – bc)(a² – b²c²) >= 0.
Aplicando la propiedad de que una diferencia de cuadrados es igual a un producto de la suma por la diferencia, esa expresión quedaría (a – bc)(a – bc)(a + bc) >= 0.
Por último, es evidente que esa expresión es positiva, ya que el factor (a – bc) aparece multiplicado por sí mismo, y el factor (a + bc) es positivo por serlo los tres números.
Siguiendo el razonamiento paso a paso, por tanto, se da la desigualdad requerida, y sólo puede darse la igualdad si a = bc, ya que en ese caso el producto vale cero, lo que corresponde a la última pregunta del problema.
Otra manera de resolver el problema es realizar un cambio de variable. Si nos fijamos bien, sólo hay un término de la desigualdad que no contiene el factor a, c/b. Si dividimos por esa expresión toda la desigualdad (que la transforma en una desigualdad equivalente, por ser c/b un número positivo), queda a²/(b²c²) – a/cb >= 1 – cb/a, que sólo depende de a/cb.
Es decir, que si cambiamos a/cb por x, donde x es un número positivo, la desigualdad se transforma en x² – x >= 1 – 1/x, que sólo depende de este número.
Si multiplicamos ahora por x, tenemos la desigualdad polinómica x³ – x² >= x – 1, que es posible estudiarla de varias formas (factorizándola, o buscando el valor mínimo del polinomio diferencia entre las dos expresiones).
Una vez que tenemos que el valor mínimo se obtiene en x = 1 y que vale 0, tenemos que la igualdad sólo se da cuando x = 1, es decir, cuando a = bc.
Otro cambio, propuesto por el colaborador de esta página Javier Nistal, es hacer el cambio cb = x, y solucionarlo entonces como una inecuación de segundo grado con parámetro a. Efectivamente, queda al final que la desigualdad sólo se alcanza si cb = x = a.
