Problema 3 del sábado de la Fase Local de la LV OME 2019 Se dirige a una edad de: 16-17 años
Consideramos un triángulo ABC y un punto D en el lado AC.
Si la longitud de AB y de DC es 1, el ángulo DBC es de 30º, y ABD es de 90º, calcula la longitud de AD.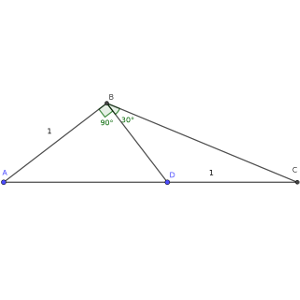
Solución:
Puesto que tenemos un triángulo rectángulo, es bastante sencillo plantearnos cómo serían las relaciones trigonométricas en él, de forma que podamos aplicarlas a los diferentes triángulos que salgan en el dibujo.
Supongamos que la longitud a calcular, la de AD, es x. Como es la hipotenusa del triángulo ABD, visto desde el ángulo DAB, el coseno de ese ángulo es 1/x.
Aplicando el teorema del coseno al triángulo ABC (si aún no conoces el teorema del coseno, también se puede conseguir un efecto similar dividiendo el lado AC por la altura y eliminando en las igualdades por pitágoras las variables internas al triángulo, pero es más costoso), llegamos a que z² = (x + 1)² + 1² – 2(x + 1)1·1/x = x² + 2x + 2 – (2x + 2)/x, donde z es la longitud de BC.
Por otra parte, si nos fijamos en el ángulo BDA, es 90 – DAB, y por tanto el ángulo BDC es 90 + DAB. Al ser un ángulo perpendicular a DAB, su seno es el coseno de DAB, de nuevo 1/x. Aplicando ahora al triángulo BDC el teorema del seno (si no lo has visto, sencillamente proviene de dividir de nuevo el triángulo en dos por la altura y comparar la altura vista desde ambos ángulos), tendremos que z/sen(BDC) = 1/sen(30), de forma que zx = 2. De aquí, obtenemos que z= 2/x.
Sustituyendo z en la ecuación primera que hemos obtenido, tenemos la igualdad 4/x² = x² + 2x + 2 – (2x + 2)/x. Si eliminamos denominadores y paréntesis, queda 4 = x⁴ + 2x³ + 2x² – 2x² – 2x. Anulando una de los extremos a cero, tenemos que 0 = x⁴ + 2x³ – 2x – 4.
Para buscar las posibles soluciones de esa ecuación de cuarto grado, podemos tratar de encontrar una factorización tanteando mediante Rufini con divisores de 8 (o sacando factor común por términos de grado similar, hasta ver que x + 2 es factor común), logrando ver que 0 = (x + 2)(x³ – 2) es equivalente al polinomio. Puesto que es imposible que x sea negativo, sólo puede ser que x³ sea 2, es decir, que x = 2^(1/3) (raíz cúbica de 2).
Este resultado es sorprendente, pues aparece una raíz cúbica en una construcción geométrica. Lamentablemente, es una construcción imposible de hacer con regla y compás exclusivamente, como se demostró hace ya muchos años, pues la raíz cúbica de 2 no es construible.