Solución al menor de los máximos
Problema 5 de la Fase Nacional de la de la LV OME 2019 Se dirige a una edad de: 16-17 años
Se consideran todos los pares de números reales (x, y) tales que 0 ≤ x ≤ y ≤ 1.
Sea M(x, y) el máximo valor del conjunto de tres números reales A = {xy, xy – x – y + 1, x + y – 2xy}.
Hallar el mínimo valor que puede tomar M(x, y) para todos estos pares (x, y).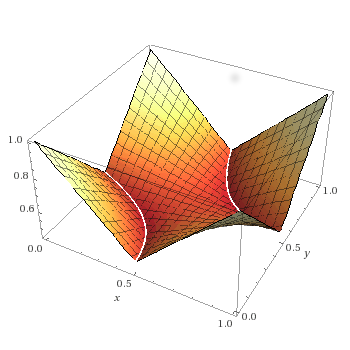
Solución:
(more…)
El menor de los máximos
Problema 5 de la Fase Nacional de la de la LV OME 2019 Se dirige a una edad de: 16-17 años
Se consideran todos los pares de números reales (x, y) tales que 0 ≤ x ≤ y ≤ 1.
Sea M(x, y) el máximo valor del conjunto de tres números reales A = {xy, xy – x – y + 1, x + y – 2xy}.
Hallar el mínimo valor que puede tomar M(x, y) para todos estos pares (x, y).
Solución: Aquí.
Solución a función entera
Problema 1 de la 60 Olimpiada Internacional (2019) Se dirige a una edad de: 17-19 años
Sea Z el conjunto de los números enteros.
Determinar todas las funciones f:Z → Z tales que, para todos los enteros a y b, f(2a) + 2f(b) = f(f(a + b)).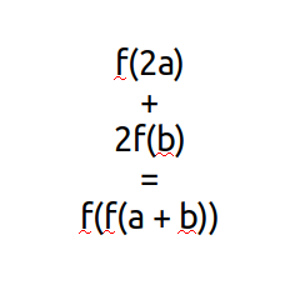
Solución:
(more…)
Función entera
Problema 1 de la 60 Olimpiada Internacional (2019) Se dirige a una edad de: 17-19 años
Sea Z el conjunto de los números enteros.
Determinar todas las funciones f:Z → Z tales que, para todos los enteros a y b, f(2a) + 2f(b) = f(f(a + b)).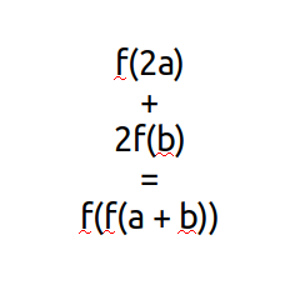
Solución: Aquí.
Solución a piezas de madera
Problema 4 del nivel C de la Fase Comarcal de la de la XXX OMCV 2019 Se dirige a una edad de: 10-11 años
¿Cuáles de las figuras A, B, C y D indicadas pueden construirse pegando por los lados piezas de madera iguales a la forma de la izquierda?
Dejo dibujado un cuadriculado de guía para facilitar el razonamiento.
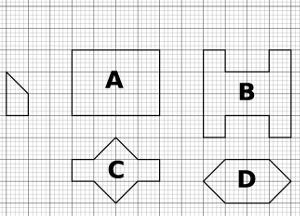
Solución:
(more…)
Piezas de madera
Problema 4 del nivel C de la Fase Comarcal de la de la XXX OMCV 2019 Se dirige a una edad de: 10-11 años
¿Cuáles de las figuras A, B, C y D indicadas pueden construirse pegando por los lados piezas de madera iguales a la forma de la izquierda?
Dejo dibujado un cuadriculado de guía para facilitar el razonamiento.

Solución: Aquí.
Solución a zona sombreada
Problema 4 del nivel B de la Fase Comarcal de la de la XXX OMCV 2019 Se dirige a una edad de: 14-15 años
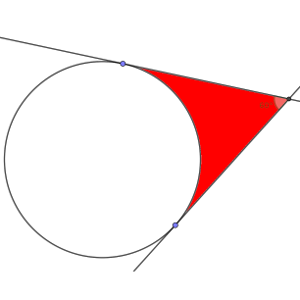
Partimos de un círculo de radio 4 metros.
Desde un punto exterior al círculo, trazamos dos tangentes al mismo, y comprobamos que forman en ese punto un ángulo de 60º.
Si rellenamos de color el área entre las dos tangentes y el círculo ¿qué área queda sombreada?
Solución: (more…)
Zona sombreada
Problema 4 del nivel B de la Fase Comarcal de la de la XXX OMCV 2019 Se dirige a una edad de: 14-15 años
Partimos de un círculo de radio 4 metros.
Desde un punto exterior al círculo, trazamos dos tangentes al mismo, y comprobamos que forman en ese punto un ángulo de 60º.
Si rellenamos de color el área entre las dos tangentes y el círculo ¿qué área queda sombreada?

Solución: Aquí.
Solución a los muñecos
Problema 4 de nivel A de la Fase Comarcal de la de la XXX OMCV 2019 Se dirige a una edad de: 12-13 años
Daniel tiene la misma cantidad de vaqueros, indios, soldados y caballeros.
Después de la visita de su primo Quique, descubre que le ha desaparecido la tercera parte de los muñecos.
Sabiendo que la cantidad de vaqueros que le queda coincide con la de los indios que le faltan, y que le quedan 14 soldados de los 21 que tenía inicialmente, ¿cuántos caballeros se ha llevado Quique?

Solución:
(more…)