Problema 1 de la 60 Olimpiada Internacional (2019) Se dirige a una edad de: 17-19 años
Sea Z el conjunto de los números enteros.
Determinar todas las funciones f:Z → Z tales que, para todos los enteros a y b, f(2a) + 2f(b) = f(f(a + b)).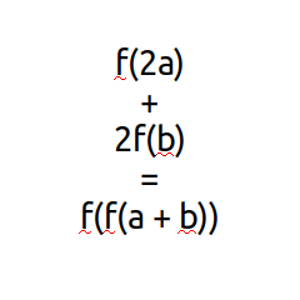
Solución:
Como siempre en este tipo de problemas complejos, voy a intentar explicar cómo se puede llegar a una solución mediante experimentación y razonamiento, pero también voy a incluir la solución que me ha enviado nuestro colaborador Javier Nistal, ya que tiene variantes interesantes.
Puesto que emplea la operación de multiplicar por 2, está claro que va a jugar un papel importante el caso en que a = 0. La expresión quedaría como f(0) + 2f(b) = f(f(b)). Y en el caso especial en que b también vale 0, tendríamos que f(0) + 2f(0) = 3f(0) = f(f(0)).
El siguiente paso que es razonable dar es imaginar un valor concreto para f(0), y jugar a “rellenar” los demás valores, a no ser que demos con una idea interesante.
Si f(0) = 1, por ejemplo, tendremos que 3f(0) = 3 = f(f(0)) = f(1), por lo que f(1) = 3.
Pero también f(0) + 2f(1) = f(f(1)), por lo que 1 + 6 = 7 = f(3). Y, claro, f(2) + 2f(0) =f(f(1)), por lo que f(2) = 7 – 2 = 5. Da la sensación de que f(n) = 2n + 1.
Para 5 podemos usar que f(2) + 2f(1) = f(f(2)), de donde 5 + 6 = 11 = f(5).
Para el 4 podemos usar f(4) + 2f(0) = f(f(2)), es decir, f(4) = f(5) – 2 = 9.
Para el 7 podemos usar f(4) + 2f(1) = f(f(3)), de donde 9 + 6 = 15 = f(7).
Para el 6, f(6) + 2f(0) = f(f(3)), por lo que f(6) = f(7) – 2 = 13.
Así, si para un cierto número impar positivo 2n + 1 lo tenemos comprobado, y para todos los anteriores, entonces, f(2n) + 2f(1) = f(f(n + 1)), es decir, 4n + 1 + 6 = f(2n + 3), con lo que ciertamente 2(2n + 3) + 1 = 4n + 7, y además f(2n + 2) + 2f(0) = f(f(n + 1)), por lo que f(2n + 2) = f(2n + 3) – 2 = 4n + 7 – 2 = 4n + 5, es decir, que f(2n + 2) = 2(2n + 2) + 1.
¿Y qué pasa con los números negativos? Pues que si tenemos un número negativo de la forma –n, entonces f(2n) + 2f(–n) = f(f(0)), por lo que 4n + 1 + 2f(–n) = 3, por lo que 2f(–n) = –4n + 2, y f(–n) = –2n + 1, así que sigue cumpliéndose que f(–n) = 2(–n) + 1.
Es decir, que si f(0) = 1, la función es exactamente f(n) = 2n + 1. Es sencillo comprobar que en ese caso se cumple la condición requerida, ya que f(2a) + 2f(b) = 4a + 1 + 2(2b + 1) = 4a + 4b + 3, mientras que f(f(a + b)) = 2(2(a + b) + 1) +1 = 2(2a + 2b + 1) + 1 = 4a + 4b + 2 + 1. Por lo tanto esta función es una de las que nos piden.
¿Habrá más funciones de la forma cx + d? Basta comprobar la identidad, así que f(2a) + 2f(b) = 2ca + d + 2(cb + d) = 2ca + 2cb + 3d, mientras que f(f(a + b)) = c(c(a + b) + d) + d = c(ca + cb + d) + d = c²a + c²b + cd + d, de forma que se tiene que dar 2ca + 2cb + 3d = c²a + c²b + cd + d para todos los valores enteros de a y de b, por lo que 3d = cd + d, es decir, 2d = cd, y además 2c = c². Este par de condiciones se cumplen si c = 2, para cualquier valor de d, y si c = 0 y d = 0.
Así, tenemos la función f(n) = 0, y la familia f(n) = 2n + d. Es sencillo comprobar que tanto una como las otras cumplen la condición requerida, pero ¿son las únicas que lo hacen, o habrá más?
Para f(n) = 0, tenemos que f(2a) + 2f(b) = 0 + 2·0 = 0, mientras que f(f(a + b)) = 0.
Para f(n) = 2n + d, tenemos que f(2a) + 2f(b) = 4a + d + 2(2b + d) = 4a + 4b + 3d, mientras que f(f(a + b)) = 2(2(a + b) + d) +d = 2(2a + 2b + d) + d = 4a + 4b + 2d + d = 4a + 4b + 3d.
El paso más delicado es el que seguimos para probar que no hay más, tratando de ver que las funciones que cumplen esa condición son siempre afines, es decir, tienen un crecimiento siempre regular.
Por ejemplo, podemos tratar de relacionar f(n) y f(n + 1), ya que f(2) + 2f(n) = f(f(n + 1)), y f(0) + 2f(n + 1) = f(f(n + 1)), es decir, son iguales. Por eso, f(2) + 2f(n) = f(0) + 2f(n + 1), así que 2f(n + 1) – 2f(n) = f(2) – f(0), o, dicho de otra forma, f(n + 1) – f(n) = (f(2) – f(0))/2, es decir, una constante.
En la solución de Javier, observa de manera similar, para a = 0, b = a, que f(0) + 2f(a) = f(f(a)). Por otra parte, si b = 0, f(2a) + 2f(0) = f(f(a)), por lo que 2f(a) = f(2a) + f(0).
Pero, volviendo a la expresión inicial, tenemos que f(2a) + 2f(b) = f(f(a + b) = f(0) + 2f(a + b), por lo que 2f(a) – f(0) + 2f(b) = f(0) + 2f(a + b), y de ahí, f(a) + f(b) = f(a + b) + f(0).
En el caso a = 1, b = 2, tenemos que f(1) + f(2) = f(3) + f(0), y también f(2) = 2f(1) – f(0), por lo que f(3) = 3f(1) – 2f(0). De forma similar, tenemos que f(4) = 4f(1) – 3f(0).
Hacemos la hipótesis de que f(n) = nf(1) – (n – 1)f(0) = n(f(1) – f(0)) + f(0).
Usando esas dos propiedades previas, se puede demostrar de manera sencilla por inducción, ya que podemos sumar 1 a cualquier valor y pasar al siguiente. Deberíamos hacer también hacer inducción hacia los valores negativos, pero eso no supone más que una pequeña complicación adicional.
Cuando tenemos demostrado este resultado, lo que tenemos es una fórmula que prueba que f(n) =cn + d, es decir, que se trata de funciones lineales. Y de ahí concluimos el resultado anterior, que c = 2 y d puede ser cualquier valor, o bien, c = d = 0 (con lo que tenemos la función nula f(n) = 0 , y la familia f(n) = 2n + d. Y que esas funciones, como hemos visto, verifican la condición.