Problema 1 de la prueba Putnam para estudiantes de grado (2018) Se dirige a una edad de 18-22 años
Encuentra todos los pares ordenados (a, b) de enteros positivos para los que se cumple 1/a + 1/b = 3/2018.
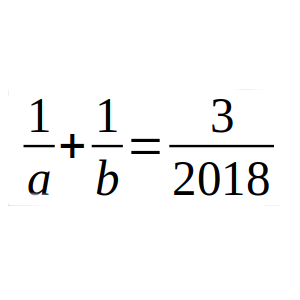
Solución:
La competición Putnam es una prestigiosa prueba de matemáticas en la que participan estudiantes de muchas universidades americanas (de Estados Unidos y de Canadá). La organiza la asociación Mathematical Asotiation of America (MAA), el primer sábado de diciembre desde 1938, y otorga diversos premios tanto individuales como a las universidades de procedencia. Podemos encontrar más información en la web de la MAA (www.maa.org).
Me llamó la atención este problema, que no parecía tan difícil como otros destinados a participantes más jóvenes. Vamos a ver cómo se puede abordar.
Como en otras ocasiones, nuestro colaborador Javier Nistal nos manda una solución propia, que incluyo al final.
Para trabajar con variable entera, una de las opciones es eliminar los denominadores, reduciendo a denominador común y eliminando éste, con lo que queda 2018b + 2018a = 3ab. A partir de ahí, puesto que se trata de una ecuación de segundo grado, deberíamos tratar de factorizarla para poder abordarla como una de primer grado.
Dejamos esta ecuación como 3ab – 2018a – 2018b = 0. Si el primer término debe aparecer como el producto de dos expresiones de primer grado, uno de los términos debería ser, por ejemplo, 3a, y el otro b, es decir, que 3ab – 2018a – 2018b debería ser similar a (3a + t)(b + s). Pensando que debemos obtener -2018b, t debe ser -2018, y como 2018 no es múltiplo de 3, s debe ser la fracción negativa -2018/3. Pero en ese caso, falta un cuarto sumando, que sería el producto de t y s, es decir, 2018²/3.
De esta forma, si sumamos ese término a la igualdad que tenemos (en artofproblemsolving llaman a esta estrategia de forma abreviada SFFT, el truco de factorización favorito del doctor Simon), tendríamos que 3ab – 2018a – 2018b + 2018²/3 = 2018²/3, es decir, que (3a – 2018)(b – 2018/3) = 2018²/3.
Como no queremos tener fracciones, multiplicamos por 3 a ambos lados (recuerda que si multiplicamos un producto, basta multiplicar uno de los factores, pero que si es una suma, debemos multiplicar ambos), y tenemos la expresión (3a – 2018)(3b – 2018) = 2018².
Ahora, estudiemos el número 2018² y todas sus posibles factorizaciones. Probablemente, no todas ellas den valores adecuados para a y b, y también deberemos tener en cuenta que a y b deben ser positivos. Puesto que 2018 = 2·1009, las descomposiciones serán las siguientes:
1·2018²
2·(2·1009²)
4·(1009²)
1009·4036
2018·2018
Luego estarían las mismas con ambos números negativos, y las cuatro primeras en el orden contrario, que producirían los mismos a y b.
Para calcular ahora los números, hay que tener en cuenta que en un momento determinado, deberemos dividir por 3, y para eso, el número adecuado debe ser divisible por 3. Es decir, que como 2018 tiene un resto módulo 3 de 2, 3a – 2018 debe tener un resto de 1, y 3b – 2018 también. Eso descarta las factorizaciones que tienen un factor 2 y un factor 2018, por lo que quedan las siguientes:
1· 2018², en las que a = 2019/3 = 673, y b = (2018² + 2018)/3 = 1358114 (o al contrario).
4·1009², en las que a = 2022/3 = 674, y b = (1009² + 2018)/3 = 340033 (o al contrario).
1009·4036, en las que a = (1009 + 2018)/3 = 1009 y b = (4036 + 2018)/3 = 2018 (o al contrario).
Las factorizaciones con números negativos contienen uno de los dos factores negativos y menores o iguales que 2018, con lo que los números a y b correspondientes no pueden ser positivos.
Por lo tanto, los pares ordenados son 6:
(673, 1358114), (674, 340033) y (1009, 2018), y los mismos pares en orden inverso.
En la solución de Javier, trata de mantener a y b como un producto del divisor máximo común por los factores distintivos, así a = m·a’, y b = m·b’, siendo que a’ y b’ no tienen divisores comunes. Buscamos primero los casos en que a es menor o igual, aunque b y a pueden intercambiar valores y obtenemos nuevos pares ordenados.
La igualdad de fracciones lleva a que a’b’ divide a 2018, de forma que considera los casos siguientes:
a’b’ = 1 lleva a una situación contradictoria, ya que a= 2·2018/3
De la misma forma, a’b’ = 1009 lleva a otra situación contradictoria.
a’b’ = 2018 lleva a los casos en que a = 673 y a = 674.
Y, por último, a’b’ = 2 lleva al caso en que a = 1009.
Evidentemente, los casos en los que b es menor que a son los mismos y hay que incluirlos.