Problema 5 del nivel B de la Fase Comarcal de la de la XXX OMCV 2019
Se dirige a una edad de: 14-15 años

Calcula el resultado de la siguiente operación:

2018² – 2017² + 2016² – 2015² + … + 4² – 3² + 2² – 1²

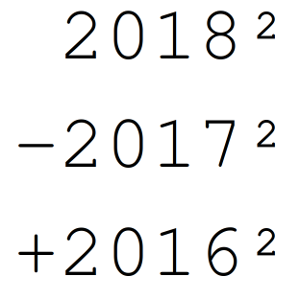
Solución:

Evidentemente, la clave consiste en expresar todas las diferencias de una forma más manejable.

Debemos recordar la expresión a² – b² = (a + b)(a – b), ya que es clave para manejar esto.

De esta forma, 2² – 1² = 3·1, 4² – 3² = 7·1, 6² – 5² = 11·1.

Generalizando , (2a)² – (2a – 1)² = (4a – 1)·1, es decir, cada pareja de cuadrados con signos diferentes se transforman realmente en una sucesión aritmética que avanza de 4 en 4, multiplicada por 1 (es decir, una sucesión aritmética a secas).

En resumidas cuentas, sólo tenemos que sumar una sucesión 3 + 7 + 11 + … + 4035, una sucesión que tiene 1009 términos (la mitad de la anterior, ya que se juntan de dos en dos).

Si conocemos la forma de sumarla directamente, lo aplicamos, y si no, la idea es sumarla dos veces, al derecho y al revés, de forma que todas las parejas sumen lo mismo, así obtendremos 1009 sumandos en el que todos dan 4035 + 3 = 4038. Como hemos sumado dos veces, la suma verdadera será la mitad, es decir, 1009·4038/2 = 2037171, que es el resultado total.