Problema 5 de la Fase Local de la LVI OME 2020 Se dirige a una edad de: 16-17 años
Sea ABC un triángulo con AB < AC y sea I su incentro. El incírculo es tangente al lado BC en el punto D.
Sea E el único punto que satisface que D es el punto medio del segmento BE.
La línea perpendicular a BC que pasa por E corta a CI en el punto P.
Demostrar que BP es perpendicular a AD.
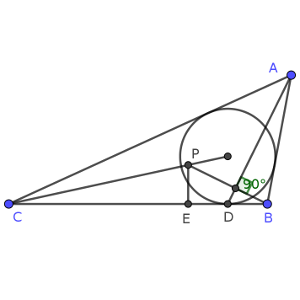
Solución:
Uno de los problemas más difíciles de los que nos podemos encontrar en la fase local. Muy poca gente creo que habrá dado con una clave que le permita probarlo, aunque hay un par de aproximaciones que funcionan.
Voy a contar dos muy diferentes. Una necesita conocer un truco algo especial, otra manejar bien ecuaciones de rectas.
La forma más sencilla de probar que dos segmentos que se cortan son perpendiculares es, curiosamente, unir sus extremos y medir los lados. Si la suma de los cuadrados de los lados contrarios da lo mismo, entonces los dos segmentos son perpendiculares.
En realidad, es una consecuencia del Teorema de Pitágoras. Si un triángulo es rectángulo, los dos lados que forman ese ángulo recto (los catetos), al cuadrado, suman lo mismo que el lado opuesto al ángulo al cuadrado.
Sin embargo, si el ángulo es agudo, los dos lados que forman ese ángulo, al cuadrado, suman más que el lado contrario al ángulo al cuadrado, mientras que si el ángulo es obtuso, sucede al contrario.
Si ahora visualizamos los cuatro trozos en los que dividimos el par de segmentos, evidentemente, forman cuatro triángulos rectángulos si se cortan perpendicularmente, y por tanto si forman un ángulo recto es evidente que sucede esa condición, pero si no forman un ángulo recto, los dos lados del cuadrilátero que están en los ángulos agudos suman menos que los cuadrados, mientras que los otros dos suman más (ambos son mayores), por lo que es imposible que sean iguales.
En nuestro dibujo, podemos tratar de comparar ambas sumas, y debido a las similitudes, podemos comparar la suma de los cuadrados.
Entonces, tenemos el cuadrilátero ABDP. Tratamos de comprobar que DP² + AB² es igual que AP² + DB².
Puesto que CI es la bisectriz del ángulo ACB, existe un punto simétrico respecto a CI de E, que podemos llamar, por ejemplo, F, y el segmento FP mide lo mismo que EP, y es perpendicular a AC como EP es perpendicular a CB.
Tenemos también que situar los puntos de tangencia a los otros dos lados de la circunferencia, pongamos M en AB y N en AC. Se observa que, debido a la simetría, CN mide lo mismo que CD, y AM que AN, y BM que BD.
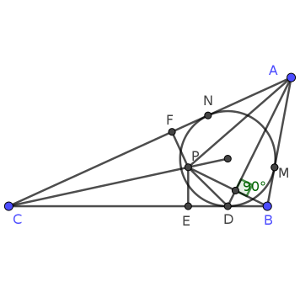
Ahora, el segmento AP es la hipotenusa del triángulo rectángulo AFP, por lo que AP² = FP² + AF², y de la misma forma, el segmento DP está en una posición similar, por lo que DP² = EP² + ED².
Además, se tiene que el segmento ED = BD = BM = FN. Puesto que AN = AM, entonces AF = AN + FN = BM + AM = AB.
por tanto DP² + AB² = DP² + AF² = EP² + ED² + AF² = FP² + ED² + AF² = FP² + BD² + AF² = BD² + AP², que es exactamente lo que se quería demostrar.
Vamos con la otra solución.
He encontrado una solución usando coordenadas para ubicar las coordenadas de los cuatro extremos de los dos segmentos, y mediante el producto escalar, ver que efectivamente son perpendiculares, pero las expresiones que he logrado son muy complicadas y es fácil cometer errores, de forma que no me parece muy conveniente. Sin embargo, la incluyo a continuación.
Cuando en pretendemos construir un triángulo en el que aparece el incentro, muchas veces resulta más sencillo empezar la construcción a partir de los puntos de tangencia y el radio de la circunferencia inscrita, para que las expresiones salgan algo más manejables. Empezar la construcción desde las coordenadas de los puntos puede ser bastante más difícil, o bien hay que conocer todas las relaciones entre las posiciones de unos y otros puntos.

Voy a situar el lado CB sobre el eje X, y poner el origen (0,0) en C (se puede hacer de cualquier otra forma y la complejidad es similar). Una forma de emplear el tiempo para asegurarse de que no te equivocas es construir al mismo tiempo una situación con valores concretos y comprobar que te da lo mismo con la expresión algebraica.
El primer parámetro que usaré será la distancia desde C al punto de tangencia (D), al que llamaré a, por ejemplo. Así, el punto D será (a, 0).
En esa recta, el siguiente punto es B, y le voy a poner (a + b, 0). El parámetro b representa la distancia del punto de tangencia a B, y según las condiciones del problema, debe ser menor que a.
El último parámetro que necesitamos es el radio de la circunferencia inscrita, y le voy a llamar r. Así, las coordenadas del incentro, I, serán (a, r).
La ecuación de la recta que une C con I, CI, será rx – ay = 0.
Para encontrar el punto de tangencia de la recta CA, que es simétrico respecto la recta CI respecto a D, levantamos una perpendicular a CI por D, ax + ry = a².
Hay que encontrar el punto de corte de las últimas dos rectas, rx – ay = 0 y ax + ry = a², por ejemplo, mediante la resolución de un sistema, x = a³/(a² + r²), y = ra²/(a² + r²).
Calculamos ahora el vector que va desde D a este último punto, (-ar²/(a² + r²), ra²/(a² + r²)) y se lo volvemos a sumar para hallar el simétrico, ((a³ – ar²)/(a² + r²), 2ra²/(a² + r²)). En nuestro dibujo anterior este punto es N.
La recta CN es la misma que CA, y tendrá de ecuación, una vez que quitemos denominadores y el factor común a, 2rax + (r² – a²)y = 0.
Por el otro lado tenemos que hacer lo mismo para encontrar M y la recta BA, de donde sacaremos A.
La ecuación de la recta que une B con I, BI, será rx + by = ra + rb.
Para encontrar el punto de tangencia de la recta BA, que es simétrico respecto la recta BI respecto a D, levantamos una perpendicular a BI por D, bx – ry = ba.
Hay que encontrar el punto de corte de las últimas dos rectas, bx – ry = ba y rx + by = ra + rb, por ejemplo, mediante la resolución de un sistema, x = (b²a + r²a + r²b)/(b² + r²), y = rb²/(b² + r²).
Calculamos ahora el vector que va desde D a este último punto, ( r²b/(b² + r²), rb²/(b² + r²)) y se lo volvemos a sumar para hallar el simétrico, ((b²a + r²a + 2r²b)/(b² + r²), 2rb²/(b² + r²)). En nuestro dibujo anterior este punto es M.
La recta BM es la misma que BA, y tendrá de ecuación, una vez que quitemos denominadores y el factor común b, 2rbx + (b² – r²)y = 2rba + 2rb².
Ya estamos listos para encontrar las coordenadas del punto A, cortando las dos rectas, x = b(a² – r²)/(ab – r²), y = 2rab/(ab – r²). Encontrar este punto exige varias simplificaciones, ya que desaparecen algunos factores en la fracción, como 2r y (a + b).
El caso es que ya estamos listos para encontrar el primer vector de los dos que necesitamos, el vector DA, que será (b(a² – r²)/(ab – r²) – a, 2rab/(ab – r²)) = (r²(a – b)/(ab – r²), 2rab/(ab – r²)). Este vector tiene la misma dirección que (r(a – b), 2ab).
El punto P, sin embargo, es mucho más sencillo de encontrar. De la construcción del problema se tiene que E es (a – b, 0) y P es un punto de la recta CI, rx – ay = 0 que tiene la misma x, es decir que r(a – b) – ay = 0, por lo que y = r(a – b)/a, y sus corrdenadas son (a – b, r(a – b)/a).
Luego el vector BP será (a – b – (a + b), r(a – b)/a) = (–2b, r(a – b)/a), que es claramente paralelo a (–2ab, r(a – b)).
Es evidente que las dos direcciones que hemos encontrado,(r(a – b), 2ab) y (–2ab, r(a – b)) son perpendiculares, como se puede comprobar por ejemplo realizando el producto escalar (o levantando un vector perpendicular a uno de ellos, y viendo que tiene la misma pendiente que el otro).