Problema 6 de la Fase Local de la LVI OME 2020 Se dirige a una edad de: 16-17 años
Sea n un entero positivo. En una cuadrícula de tamaño n × n, algunas casillas tienen un espejo de doble cara a lo largo de una de sus diagonales.
En el exterior de cada casilla de los lados izquierdo y derecho de la cuadrícula se encuentra un puntero láser, que apunta horizontalmente hacia la cuadrícula.
Los láseres se numeran de 1 a n en cada lado, en ambos casos de arriba hacia abajo.
Un láser es rojo cuando sale de la cuadrícula por el borde superior y es verde si sale de la cuadrícula por el borde inferior.
Si cada láser sale o bien por el borde inferior o por el superior, demostrar que la suma de los números con los que se numera a los láseres rojos es menor o igual que la suma de los números con los que se numera a los láseres verdes.
Solución:
Este problema sí que es complicado de verdad, pero pone de manifiesto una propiedad muy curiosa.
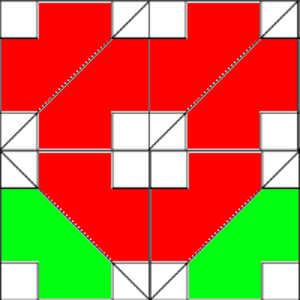
Si tratamos de poner ejemplos, veremos que hay situaciones muy complejas (por ejemplo, la siguiente a estas líneas).
En el ejemplo que viene en la cabecera, ambos láseres suman lo mismo, 1 + 2 + 3 = 6. Sin embargo, en el siguiente, vemos que los rojos suman 1 + 2 + 2 = 5, mientras que los verdes suman 1 + 3 + 3 = 7.
Es uno de los ejemplos más sencillos en la que la desigualdad es estricta. Se puede hacer uno 2×2 con la idea que viene al final del problema.
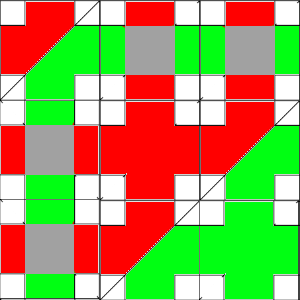
Lo que sí está claro, es que la cantidad total de láseres rojos y verdes sumada es 2n, y eso, unido al hecho de que no pueden salir por los lados horizontales, sólo por los verticales, hace que haya una relación uno a uno, es decir, que no se pueden mezclar o superponer los láseres.
Si no todos los láseres saliesen por arriba o por abajo, podrían superponerse.
No pueden salir dos por la misma casilla, ya que si hacemos el recorrido desde la salida hasta el inicio, sólo puede salir de ahí un único láser (no hay manera de separarlo en dos, de la misma forma que no hay manera de que se unan dos).
Puesto que salen dentro de una casilla (podemos suponer que en el centro), si son rojos, recorren una serie de casillas hasta salida que, en vertical, equivaldrá al menos al número que le hemos asignado (menos media).
Así, si un láser rojo sale en la casilla 2, deberá recorrer verticalmente 1 casilla y media.
Sin embargo, el verde, que debe salir por debajo, recorrerá n menos el número que se le ha asignado más media, es decir, que un láser verde que saliese de la casilla dos debería recorrer verticalmente al menos 1 y media, pero si sale desde la una, verticalmente tiene que recorrer 2 y media.
Puesto que no se superponen, el recorrido vertical debe ser en total menor que n². Y eso tiene como consecuencia lo que buscamos, de una forma un tanto extraña.
Vamos a llamar a R a la suma de todos los números de los rojos. La suma de todos los recorridos de los láseres rojos será entonces, al menos, R – n/2 (ya que a cada uno le quitamos 1/2 y hay n).
Vamos a llamar V a la suma de todos los números de los verdes. La suma de todos los recorridos de los láseres verdes será n² – V + n/2, ya que hay n y a cada uno lo restamos de n y le sumamos 1/2.
El que el recorrido vertical tenga que ser menor que n² quiere decir que R – n/2 + n² – V + n/2 <= n², pero es sencillo ver que esa desigualdad se transforma en R – V + n² <= n², y que por tanto R debe ser menor que V necesariamente.
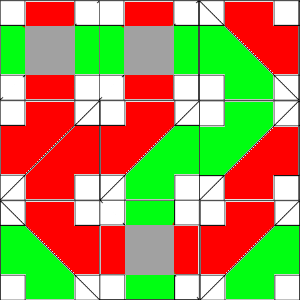
De hecho, el menor será estricto si alguno de los láseres rojos rebota en alguna ocasión hacia abajo o uno verde hacia arriba, ya que el recorrido que hace alguno de ellos verticalmente será mayor que el mínimo. Se puede comprobar en el siguiente dibujo más simple.