Problema 8 del concurso marató de problemes 2020 Se dirige a una edad de: 14-15 años
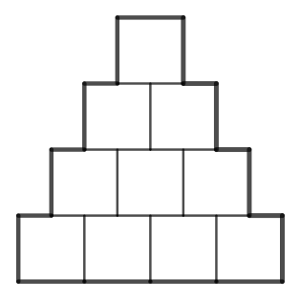
En la siguiente figura se aprecia una estructura de aspecto triangular hecha con cuadrados iguales, todos de lado 1 cm.
En la fila superior hay 1 cuadrado.
Bajo esa fila hay otra con dos cuadrados.
La tercera fila empezando desde arriba tiene tres cuadrados.
Y así sucesivamente, hasta la fila n, en la que hay n cuadrados.
La imagen corresponde a un n = 4.
Cada cuadrado recae sobre dos de los cuadrados de la fila previa, no necesariamente centrado, pero sin dejar huecos con los cuadrados vecinos.
Hay una línea negra dibujada que marca el polígono que rodea a todos estos cuadrados.
Indicamos con S la superficie de este polígono en cm² para un n determinado, y P al perímetro en cm del mismo polígono.
Se puede escribir S en función de P como un polinomio d segundo grado, independientemente del n. Esta relación se da para cualquier valor de n.
Encuentra los valores a, b, c que cumplen S = aP² + bP + c.
Solución: Aquí.