Problema 1 de la fase nacional de la 56 Olimpiada Matemática Española (2020) Se dirige a una edad de: 16-17 años
Decimos que un polinomio p(x) , con coeficientes reales, es almeriense si tiene la forma p(x) = x³ + ax² + bx + a, y sus tres raíces son números reales positivos en progresión aritmética.
Halla todos los polinomios almerienses tales que p(7/4) = 0.
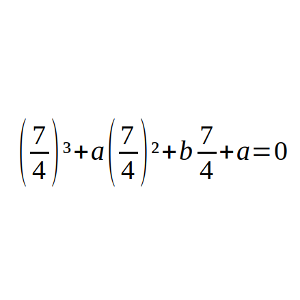
Solución:
Pongamos primero juntos nuestros objetivos y las definiciones y conceptos que vamos a utilizar.
Los polinomios almerienses tienen las tres raíces reales positivas en progresión aritmética, lo que implica que, para ciertos valores s y t, siendo t menor que s, esas raíces serán s – t, s y s + t, y podremos factorizar el polinomio de la forma p(x) = (x – s – t)(x – s)(x – s + t).
Por otra parte, p(7/4) = 0, por lo que una de las tres raíces es, precisamente, 7/4.
Además, los coeficientes de los términos de segundo y primer grado, y el término independiente son, respectivamente, a, b y a, es decir, que el término independiente es idéntico al coeficiente de segundo grado.
Aplicando las fórmulas de Cardano-Vieta (o desarrollando el producto que hemos planteado anteriormente), tenemos que a = – s + t – s + s – t = -3s, pero por otra parte a = -s(s – t)(s + t) = -s(s² – t²). Puesto que s debe ser positivo, debe darse que 3 = s² – t².
Veamos qué sucede en cada uno de los casos, según el valor de los tres que sea 7/4.
Si 7/4 = s – t, tenemos que 3 = 7/4 (s + t), por lo que el otro valor es s + t = 12/7, que es ligeramente menor que s – t, cosa que no debería ocurrir.
Si 7/4 = s + t, razonando de manera análoga, tenemos que s – t = 12/7, por lo que es fácil determinar el valor de s, que será la media aritmética, (7/4 + 12/7)/2 = 97/56. El polinomio, por tanto, será x³ – 291/56 x² + 14113/1568 x – 291/56.
Por último, si s = 7/4, tenemos que 3 = s² – t² = 49/16 – t², por lo que t² = 1/16, y como t es positivo, tenemos que t = 1/4. Así que las raíces serán 6/4, 7/4 y 8/4, y el polinomio será x³ – 21/4 x² + 73/8 x – 21/4.
Por lo que los dos únicos polinomios almerienses que cumplen la condición pedida serán x³ – 291/56 x² + 14113/1568 x – 291/56 y x³ – 21/4 x² + 73/8 x – 21/4.