Problema 7 del concurso marató de problemes 2019
Se dirige a una edad de: 14-15 años

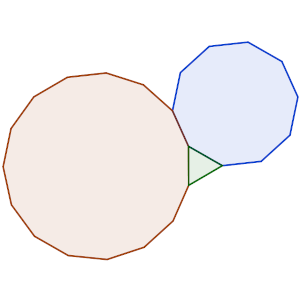
En la imagen de ejemplo podemos ver cómo podemos encajar un polígono regular de 10 lados, uno de 3 (triángulo equilátero) y otro de 15, sin dejar espacios entre ellos.

a) Estudiar y razonar con todo detalle todos los valores de m y n (pueden ser iguales, pero supondremos que m es menor o igual que n) que hacen que un polígono regular de m lados, otro de n lados y un triángulo equilátero encajan sin dejar espacio entre los tres.

b) Estudiar todos los posibles valores de m, n y p (donde m menor o igual que n, y n menor o igual que p) en los que tres polígonos regulares de tamaños m, n y p encajan sin dejar huecos.

Solución

La principal idea que debemos barajar aquí es que los ángulos interiores sumen 360º.

Es decir, necesitamos algún método de cálculo que nos permita calcular el ángulo interior de un polígono regular. En la imagen vemos que, si dividimos en triángulos desde el centro el polígono regular, los ángulos interiores son sumas de dos ángulos de un triángulo isósceles, y el ángulo central (el que es diferente en ese triángulo equilátero), dependerá sólo de cuántos lados tiene el polígono regular.

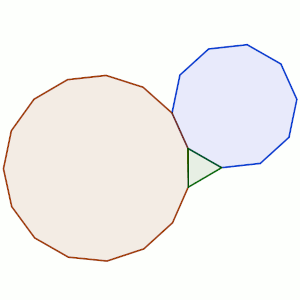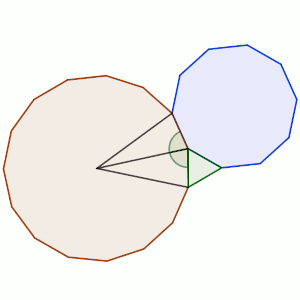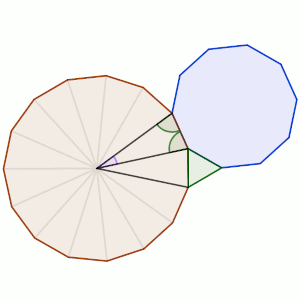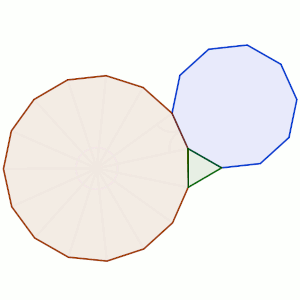
Por lo tanto, en un polígono de n lados el ángulo central medirá 360/n, y la suma de los otros dos, que será el ángulo interior, medirá 180º – 360º/n.

En el caso que nos ocupa, el ángulo interior del triángulo mide (evidentemente) 180º – 120º = 60º, el del decágono mide 180º – 36º = 144º, y el del polígono de quince lados 180º – 24º = 156º. en total, vemos que claramente suman 360º.

Vamos a preparar un listado, y trataremos de estudiar qué sumas pueden dar 360. Es muy importante, para poder terminar con éxito todas las posibilidades, que los poliedros que usemos estén ordenados por número de lados, calculando el último (el de más lados) a partir de los dos anteriores.

En el apartado a), sabemos que uno de los polígonos tiene 3 lados, y por tanto, su ángulo interior mide 60º. El segundo en tamaño de los polígonos tiene que sumar con él más de 180º. Como eso significaría tener 120º de ángulo interno (180º – 360º/n = 120º, por lo que n = 6), de be tener más de 6 lados.

Si lo unimos con uno de 7 lados, tendríamos un ángulo total de 60º + 900º/7 = 1320º/7, faltan 1200º/7 para los 360º, que corresponde a un ángulo interior de uno de 42 lados.

Si lo unimos con uno de 8 lados, tenemos un ángulo total de 60º + 135º = 195º, faltan 165º para los 360º, que corresponde a uno de 24 lados.

Si lo unimos con uno de 9 lados, tenemos un ángulo total de 60º + 140º = 200º, faltan 160º para los 360º, que corresponde a uno de 18 lados.

Si lo unimos con uno de 10 lados, tenemos un ángulo total de 60º + 144º = 204º, faltan 156º para los 360º, que corresponde a uno de 15 lados.

Si lo unimos con uno de 11 lados, tenemos un ángulo total de 60º + 1620º/11 = 2280º/11, faltan 1680º/11 para los 360º, que no corresponde a ningún polígono regular (da fracción).

Si lo unimos con uno de 12 lados, tenemos un ángulo total de 60º + 150 = 210º, faltan 150º para los 360º, que corresponde a otro de 12 lados.

Evidentemente, estas son las parejas que buscamos para el apartado a) 3 – 12 – 12, 3 – 10 – 15, 3 – 9 – 18, 3 – 8 – 24 y 3 – 7 – 42.

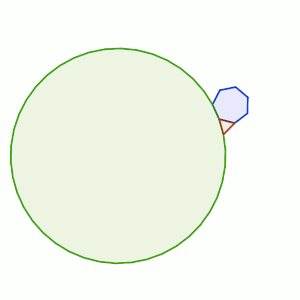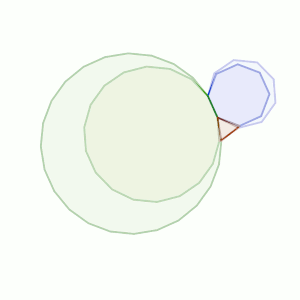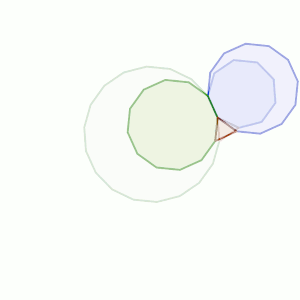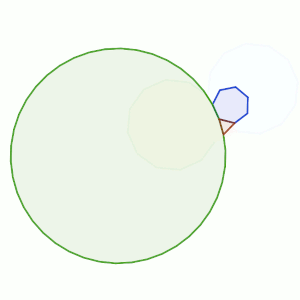
En el apartado b) hemos de buscar partiendo de un poliedro pequeño que puede ser más diverso.

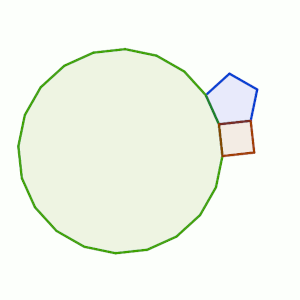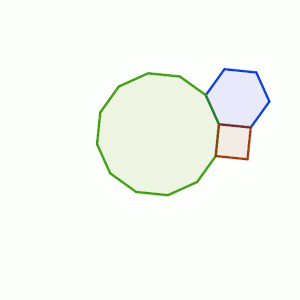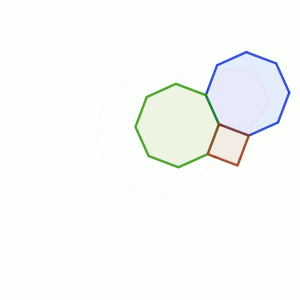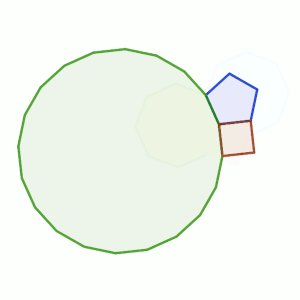
Iniciar con el cuadrado nos hace tener 90º de partida. Con otro cuadrado sólo llegamos a 180º, así que deberemos tomar polígonos mayores,

Si lo unimos con uno de 5 lados, tendríamos un ángulo total de 90º + 108 = 198º faltan 162º para los 360º, que corresponde a un ángulo interior de uno de 20 lados.

Si lo unimos con uno de 6 lados, tendríamos un ángulo total de 90º + 120º = 210º faltan 150º para los 360º, que corresponde a un ángulo interior de uno de 12 lados.

Si lo unimos con uno de 7 lados, tendríamos un ángulo total de 90º + 900º/7 = 1530º/7, faltan 990º/7 para los 360º, que no corresponde a un ángulo interior de ninguno regular (da 9,333…lados).

Si lo unimos con uno de 8 lados, tendríamos un ángulo total de 90º + 135º = 225º, faltan 135º para los 360º, que corresponde a un ángulo interior de otro de 8 lados.

Evidentemente, no hay más con cuadrados.

Iniciar con el pentágono nos hace tener 108º de partida. Con otro pentágono pasamos de 180º, así que deberemos tomar polígonos iguales o mayores,

Si lo unimos con uno de 5 lados, tendríamos un ángulo total de 108º + 108º = 216º faltan 144º para los 360º, que corresponde a un ángulo interior de uno de 10 lados.

Si lo unimos con uno de 6 lados, tendríamos un ángulo total de 108º + 120º = 228º faltan 132º para los 360º, quue no corresponde a un ángulo interior de ninguno regular (da 7,5 lados).

Si lo unimos con uno de 7 lados, tendríamos un ángulo total de 108º + 900º/7 = 1656º/7, faltan 864º/7 para los 360º, que no corresponde a un ángulo interior de ninguno regular (da 6,3636… = 70/11 lados). Además, serían ya polígonos menores que el segundo.

Evidentemente, no hay más con pentágonos.

Sigamos con hexágonos.El ángulo interior debe ser de 120º, lo mínimo que le podemos unir es 120º, y el resto debe ser 120º, así que sería con 3 polígonos iguales.

Y evidentemente no hay más, ya que el más pequeño no puede superar 360º/3 = 120º.