Problema 13 del concurso marató de problemes 2019 Se dirige a una edad de: 14-15 años
Una pirámide de base cuadrada tiene todas sus caras triangulares formadas por triángulos equiláteros, de la misma longitud L.
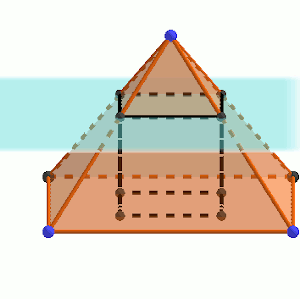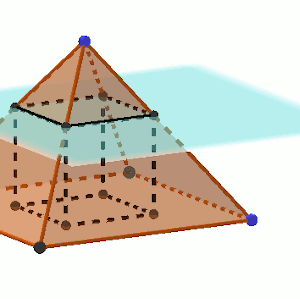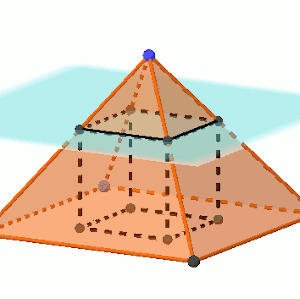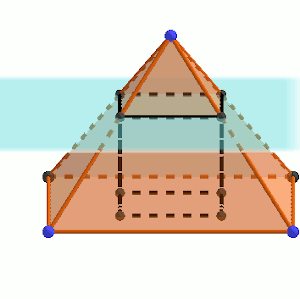
Cortamos esta pirámide por un plano paralelo a la base y proyectamos sobre la base los cuatro puntos de corte de este plano con las aristas.
De esta forma, queda definido un cubo. Podemos ver un dibujo en la imagen siguiente.
¿Qué porcentaje del volumen de la pirámide queda ocupado por este cubo?
Solución:
La proporción entre el volumen del cubo y de la pirámide es independiente del tamaño de la pirámide, ya que si escalas la pirámide, también escalas el cubo. Por tanto, voy a fijar durante todo el razonamiento esta longitud en 2 unidades para que los cálculos sean sencillos. También es posible tomar una variable 2m = L, con objeto de simplificar los cálculos, en el caso en que se decida seguir usando una variable.
Una buena decisión a la hora de tratar con figuras tridimensionales es hacer una sección plana para trabajar en plano, de forma que en esta ocasión voy a cortar por el centro del lado del cuadrado, de forma que obtendremos la altura de dos de las caras laterales como lados de la sección. También sería posible trabajar con una sección que tomara la diagonal de la base. Los cálculos serían similares, y el resultado final el mismo.
A continuación tenemos una imagen de cómo quedaría la sección, con el exterior con forma de triángulo y el cubo que se aprecia como un cuadrado inscrito en el triángulo.
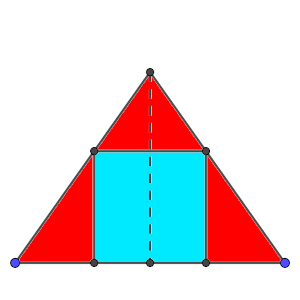
La base mide, evidentemente, 2 unidades. Las alturas de los triángulos equiláteros, si se tienen en cuenta que forman un cateto de un triángulo rectángulo que tiene una hipotenusa de 2 y otro cateto de 1, debe medir raíz(2² – 1²) = raíz(3).
Por lo tanto, el borde de nuestra sección es un triángulo isósceles con una base que mide 2 y dos lados iguales que miden raíz(3). Su altura (línea discontinua en el dibujo), que coincide con la altura de la pirámide, forma un triángulo rectángulo de hipotenusa raíz(3), y cuyo otro cateto mide 1, por lo que esta altura mide exactamente raíz(raíz(3)² – 1²) = raíz(3 – 1) = raíz(2).
Si nos fijamos en la sección cuadrada, genera dos triángulos semejantes al triángulo rectángulo descrito anteriormente. Puesto que necesitamos el lado de ese cuadrado, que coincide con el lado del cubo inscrito en la pirámide, supondremos que mide 2x, y por semejanza, tenemos que raíz(2)/1 = 2x/(1 – x), de forma que (1 – x)·raíz(2) = 2x, y por tanto raíz(2) – raíz(2)x = 2x, y tenemos que raíz(2) = 2x + raíz(2)x = (2 + raíz(2))x.
Para averiguar el valor de esa x, primero multiplicaremos por el conjugado de este coeficiente, para que la x quede multiplicada por un número entero, (2 – raíz(2)), teniendo la igualdad (2 – raíz(2))·raíz(2) = 2x. Operando, resulta que 2raíz(2) – 2 = 2x, luego x = raíz(2) – 1.
Esto significa que el lado del cubo es el doble, es decir 2raíz(2) – 2, aproximadamente 0,8284.
Calculemos ahora los volúmenes de las figuras. El volumen de la pirámide se calcula como un tercio del área de la base por la altura, es decir, 4·raíz(2)/3, aproximadamente 1,886 unidades cúbicas.
Por otro lado, el volumen del cubo será (2raíz(2) – 2)³ = 16raíz(2) – 48 + 24raíz(2) – 8 = 40raíz(2) – 56, aproximadamente 0,5685 unidades cúbicas.
El cociente de ambos números será (40raíz(2) – 56)/(4·raíz(2)/3), que es mejor racionalizar, obteniendo 30 – 21raiz(2) , aproximadamente 0,3015.
Eso quiere decir que el porcentaje del volumen de la pirámide ocupado por el cubo es del 30,15%.