Problema 3 de la Fase Local de la Olimpiada Española de Matemáticas 2021
Se dirige a una edad de: 16-17 años

En el triángulo ABC con lado mayor BC, las bisectrices se cortan en I. Las rectas AI, BI y CI cortan a BC, CA y AB en los puntos D, E y F, respectivamente.
Se consideran puntos G y H, en los segmentos BD y CD, respectivamente, tales que el ángulo GID es igual a ABC, y HID es igual a ACB. Probar que BHE = CGF

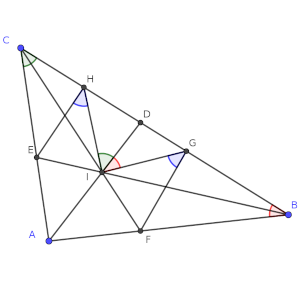
Solución:

Una vez dibujamos lo que sabemos y nuestro objetivo, es hora de marcar ángulos.

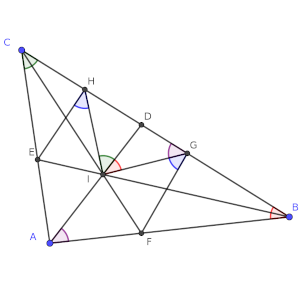
El ángulo DAB, que es la mitad de CAB (no olvidemos que las rectas que se cortan son las bisectrices) también se repite en DGI, ya que el triángulo DAB y el DGI coinciden en el ángulo D, es decir, tienen ese ángulo igual, pero también en el ángulo DIG, que es el mismo que DBA. De hecho, son triángulos semejantes, sólo que están en una posición invertida.

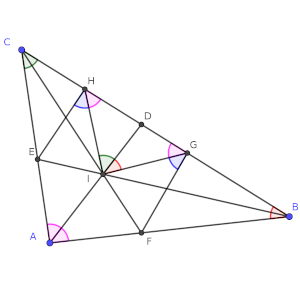
Repitiendo el razonamiento al otro lado, con los triángulos DAC y DIH, tendríamos que el ángulo DHI es igual que el CAD, que de nuevo es la mitad de CAB.

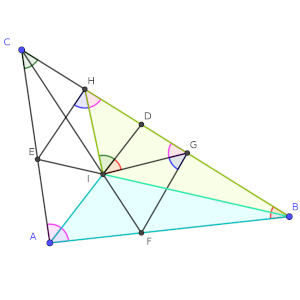
Una vez razonado este punto, es sencillo ver que los triángulos BIH y BIA son simétricos, es decir, son idénticos, así que los puntos A y H son simétricos, y el ángulo EHI es, realmente, idéntico a CAD. De la misma forma, IGF es igual, y por tanto entre sí son iguales.

Este problema, aunque se pueda explicar de manera sencilla, no es tan fácil como cabría esperar, ya que hay que trabajar en ir buscando ángulos repetidos y completar triángulos hasta encontrar alguna igualdad que nos permita llegar a las conclusiones.

Se puede trabajar con varios razonamientos similares. Al final, GI y HI son bisectrices de DHE y FGD, que a su vez son copia de CAB. Y eso se puede probar de diversas formas.