Problema 3 del nivel B fase autonómica de la Olimpiada de la Comunidad Valenciana 2019 Se dirige a una edad de: 14-15 años
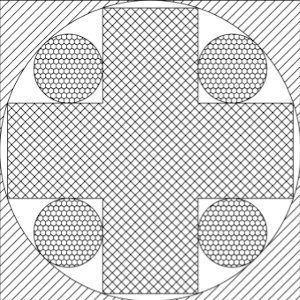
El siguiente diseño es el diseño de una baldosa de 20 cm de lado.
Calcula el valor de la superficie de las diferentes áreas de diferente sombreado (zona 1, rallada, zona 2, en blanco, zona 3, panal, y zona 4, cuadrícula).
Solución:
Es más difícil de lo que parece, y debemos usar en primer lugar todos los radios posibles a zonas de contacto entre circunferencias y figuras rectas.
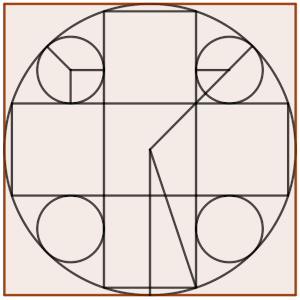
Empecemos por encontrar el lado de la cruz (l), que está formada por cinco cuadrados.
Se aprecia que, desde el centro del cuadrado del centro, que coincide con el centro de la circunferencia de radio 10 cm, se forma un triángulo rectángulo de hipotenusa 10 y catetos 3l/2 y l/2 (funciona mejor si tomamos x = l/2). Se cumple, por tanto, la fórmula del Teorema de Pitágoras, y 100 = 9l²/4 + l²/4 = 10l²/4, por lo que 40 = l², y así l = 2·raíz(10) (es decir, x = raíz(10)).
Si trabajamos con decimales, l = 6,325 y x =3,162.
Es mucho más difícil calcular el radio de las circunferencias pequeñas, r. Dada la simetría de la figura, el centro de la circunferencia grande, el centro de la pequeña y el punto de tangencia están alineados (si no, sería mucho más difícil), y se puede formar un pequeño cuadrado de lado r cuya diagonal está sobre ese radio.
Dado que ahí se forma un triángulo rectángulo, tenemos que su diagonal d cumple que d² = r² + r², es decir, que d = raíz(2)·r.
De la misma forma, el trozo que queda del radio mayor antes de este cuadrado mediría raíz(2)·x = 2·raíz(5).
Y como se puede apreciar en el dibujo, dada la alineación mencionada, 10 = 2·raíz(5) + raíz(2)·r + r, de donde sabemos que 10 – 2·raíz(5) = (raíz(2) + 1)·r, por lo que r = (10 – 2·raíz(5))/(raíz(2) + 1) = 10·raíz(2) + 2·raíz(5) – 2·raíz(10) – 10, usando multiplicación por el conjugado, o bien 2,290 si usamos aproximación decimal.
Una vez que tenemos hechos esos cálculos, pasemos a dar las áreas pedidas:
Zona 1 (rallada): 20² – Pi·10² = 400 – 100·Pi, aproximadamente 85,84 cm².
Zona 2 (en blanco): Pi·10² – 5·(2·raíz(10))² – 4·Pi·(10·raíz(2) + 2·raíz(5) – 2·raíz(10) – 10)², aproximadamente 48,28 cm².
Zona 3 (panal): 4·Pi·(10·raíz(2) + 2·raíz(5) – 2·raíz(10) – 10)², aproximadamente 65,88 cm².
Zona 4 (cuadrícula): 5·(2·raíz(10))², exactamente 200 cm².