Problema 1 de la fase catalana de la 57 Olimpiada Matemática Española (2020/21)
Se dirige a una edad de: 16-17 años

Sean a y b dos números reales tales que 1010 ≤ a, b ≤ 2020.

Demuestra que (a + b)(1/a + 1/b) ≤ 9/2.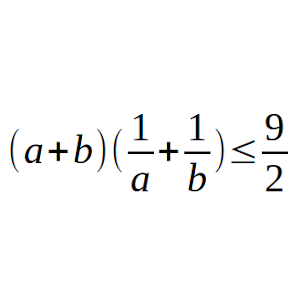
Solución:

Realizando la operación algebraica, la desigualdad que tenemos sería equivalente a la siguiente: a/a + a/b + b/a + b/b ≤ 9/2, es decir, a/b + b/a ≤ 5/2. Sin embargo como, a/b y b/a son inversos, si llamamos x = a/b, la desigualdad es equivalente a x + 1/x ≤ 5/2, es decir, x + 1/x – 5/2 ≤ 0.

El número x = a/b es un número positivo, que está entre 1/2 y 2, ya que el menor valor que puede tomar a es 1010 y el mayor que puede tomar b es 2020, y también sucede al revés. Si conseguimos trabajar con la expresión obtenida anteriormente y factorizarla, podremos saber si la desigualdad es o no cierta.

Reduciendo a común denominador, tenemos que la (2x² + 2 – 5x)/(2x) ≤ 0. El polinomio 2x² – 5x + 2 tiene las raíces (5 + raíz(25 – 16))/4 = (5 + 3)/4 = 2 y (5 – raíz(25 – 16))/4 = (5 – 3)/4 = 1/2, por lo que podemos escribir la desigualdad como 2(x – 2)(x – 1/2)/(2x) ≤ 0, es decir, como (x – 2)(x – 1/2)/x ≤ 0.

Veamos el signo de la expresión (x – 2) es negativo, ya que x = a/b es siempre menor que 2, como hemos visto anteriormente, la expresión (x – 1/2) sin embargo es positiva, ya que x siempre es mayor que 1/2, y x, el denominador, es claramente positivo.

Por lo tanto se verifica que (x – 2)(x – 1/2)/x ≤ 0, lo que es equivalente a la expresión que buscamos, (a + b)(1/a + 1/b) ≤ 9/2.